
| A. | 必要不充分 | B. | 充要 | C. | 充分不必要 | D. | 不充分不必要 |
分析 根据椭圆的定义和性质,利用充分条件和必要条件的定义进行判断即可.
解答 解:若方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆,则满足$\left\{\begin{array}{l}{5-m>0}\\{m+3>0}\\{5-m≠m+3}\end{array}\right.$,即$\left\{\begin{array}{l}{m<5}\\{m>-3}\\{m≠1}\end{array}\right.$,
即-3<m<5且m≠1,此时-3<m<5成立,即充分性成立,
当m=1时,满足-3<m<5,但此时方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1即为x2+y2=4为圆,不是椭圆,不满足条件.即必要性不成立.
故“方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆”是“-3<m<5”的充分不必要条件.
故选:C.
点评 本题主要考查充分条件和必要条件的判断,考查椭圆的标准方程,根据椭圆的定义和方程是解决本题的关键,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | l∥α | B. | l⊥α | ||
| C. | l?α | D. | l与α相交但不垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
| A. | 24 | B. | 35.6 | C. | 40 | D. | 40.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{7}}{7}$或$\frac{5}{7}$ | D. | $\frac{5}{7}$或$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
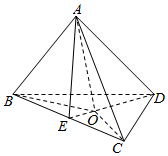 在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.
在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 等边三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com