
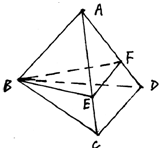
 已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:
已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:| DF |
| DB′ |
| DB′ |
| AD |
| a |
| 2 |
| EF |
| CD |
| AF |
| AD |
| a |
| 2 |
| 3a |
| 2 |
| 3a |
| 4 |
| 3 |
| 4 |
| 11a |
| 4 |
| x |
| 2 |
| 1 |
| 4 |
| x |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 4 |
| ||
| 8 |
| 7 |
| 8 |
| ||
| 8 |
| 7 |
| 8 |
7
| ||
| 32 |
| 17 |
| 32 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
7
| ||
| 32 |
| ||
| 4 |
| 17 |
| 32 |
| 1 |
| 4 |
| 11 |
| 16 |
| 3x |
| 2 |
3
| ||
| 16 |
| x |
| 2 |
| 3x |
| 2 |
| 1 | ||
|
3a
| ||
| 8 |
| 3a |
| 4 |
| 3x |
| 2 |
| EF |
| 2 |
| 11 |
| 16 |
| 3a |
| 8 |
| 3a |
| 4 |
2a2-(
| ||
| 2a2 |
| 23 |
| 32 |
| ||
| 8 |
| ||
| 8 |
| ||
| 4 |


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
| A、A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 | ||||
| B、科学家利用鱼的沉浮原理制造潜艇 | ||||
C、由圆x2+y2=r2的面积πr2,猜出椭圆
| ||||
| D、由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、没有公共点的两条直线 |
| B、分别位于两个不同平面的两条直线 |
| C、某一平面内的一条直线和这个平面外的一条直线 |
| D、不同在任何一个平面内的两条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、垂直于同一直线的两条直线 |
| B、顺次首尾相连的四条线段 |
| C、两两相交的三条直线 |
| D、分别在两条异面直线上两点连线的中点的轨迹 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com