
| A. | (-2,0) | B. | (-2,-1) | C. | (-$\frac{5}{4}$,0) | D. | (-$\frac{5}{4}$,-1) |
分析 先将函数进行换元,转化为一元二次函数问题.同时在结合函数f(x)的图象,确定b的取值范围.
解答 解:令t=f(x),则原函数方程等价为t2+bt+$\frac{1}{4}$=0.
作出函数f(x)的图象如图1:
图象可知当由0<t<1时,函数t=f(x)有3个交点.
所以要使f2(x)+bf(x)+$\frac{1}{4}$=0有六个相异实根,
则等价为有两个根t1,t2,
且0<t1<1,0<t2<1.
令g(t)=t2+bt+$\frac{1}{4}$,
则由根的分布(如图2)可得$\left\{\begin{array}{l}{△>0}\\{f(0)=\frac{1}{4}>0}\\{f(1)=1+b+\frac{1}{4}>0}\\{0<-\frac{b}{2}<1}\end{array}\right.$,即$\left\{\begin{array}{l}{{b}^{2}-1>0}\\{b>-\frac{5}{4}}\\{-2<b<0}\end{array}\right.$,即$\left\{\begin{array}{l}{b>1或b<-1}\\{b>-\frac{5}{4}}\\{-2<b<0}\end{array}\right.$,
解得-$\frac{5}{4}$<b<-1,
则实数b的取值范围是(-$\frac{5}{4}$,-1).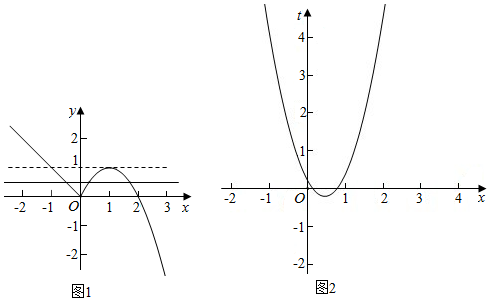
故选:D.
点评 本题考查复合函数零点的个数问题,以及二次函数根的分布,解决本题的关键是利用换元,将复合函数转化为我们熟悉的二次函数,换元是解决这类问题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,10] | B. | [5,10] | C. | [8,+∞) | D. | [8,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
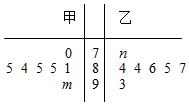 如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( )
如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( )| A. | a>b | B. | a<b | ||
| C. | a=b | D. | a,b的大小与m,n的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2×(31008-1) | B. | 2×31008 | C. | $\frac{{{3^{2016}}-1}}{2}$ | D. | $\frac{{{3^{2016}}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com