
分析 (Ⅰ)化圆的一般式方程为标准式,求出圆心坐标和半径,然后分切线的斜率存在和不存在求解,当斜率不存在时直接写出切线方程,斜率存在时,设出切线方程的点斜式,化为一般式,由圆心到切线的距离等于半径求斜率,则曲线方程可求;
(Ⅱ)曲线x2+y2+2x-6y-6=0上有两点P、Q,满足关于直线x+my+4=0对称,说明曲线是圆,直线过圆心,易求m的值;设P(x1,y1)、Q(x2,y2),PQ方程为y=-x+b.联立方程组,结合韦达定理,以及满足$\overrightarrow{OP}•\overrightarrow{OQ}$=-7,求得k的方程,然后求直线PQ的方程;
(Ⅲ)过点N(2,3)的弦AB分它的斜率存在、斜率不存在两种情况分别求得△ABC的面积S的值,综合可得△ABC的最大面积以及此时直线AB的斜率.
解答 解:(Ⅰ)∵圆C的方程为x2+y2+2x-6y-6=0,
即(x+1)2+(y-3)2 =16,表示以C(-1,3)为圆心,半径r=4的圆.
当过点M(-5,11)的圆的切线斜率存在时,
设切线为y-11=k(x+5),即kx-y+5k+11=0.
根据圆心C(-1,3)到切线的距离等于半径4,
可得$\frac{|-k-3+5k+11|}{\sqrt{{k}^{2}+1}}$=4,求得 k=-$\frac{3}{4}$,
故切线的方程为-$\frac{3}{4}$x-y+5•(-$\frac{3}{4}$)+11=0,即 即3x+4y-29=0.
当过点M(-5,11)的圆的切线斜率不存在时,切线的方程为x=-5.
综上可得,过点M(-5,11)的圆C的切线方程为即3x+4y-29=0 或x=-5.
(Ⅱ)由题意可得,圆心(-1,3)在直线x+my+4=0上,
∴-1+3m+4=0,求得m=-1,
即直线PQ与直线y=x+4垂直,
∴设P(x1,y1)、Q(x2,y2),PQ方程为y=-x+b.
将直线y=-x+b代入圆方程,得2x2+2(4-b)x+b2-6b-6=0.
△=4(4-b)2-4×2×(b2-6b-6)>0,得2-4$\sqrt{2}$<b<2+4$\sqrt{2}$.
由韦达定理得x1+x2=-(4-b),x1•x2=$\frac{{b}^{2}-6b-6}{2}$.
y1•y2=b2-b(x1+x2)+x1•x2=$\frac{{b}^{2}}{2}$+b-3.
∵$\overrightarrow{OP}•\overrightarrow{OQ}$=-7,∴x1x2+y1y2=-7,即b2-2b+1=0.
解得b=1∈(2-4$\sqrt{2}$,2+4$\sqrt{2}$).
∴所求的直线方程为y=-x+1.
(Ⅲ)过点N(2,3)作直线与圆C交于A,B两点,
当AB的斜率不存在时,AB的直线方程为x=2,
此时,CN⊥AB,且CN=3,AB=2$\sqrt{{CA}^{2}{-CN}^{2}}$=2•$\sqrt{16-9}$=2$\sqrt{7}$,
△ABC的面积S=$\frac{1}{2}$•AB•CN=$\frac{1}{2}$•2$\sqrt{7}$•3=3$\sqrt{7}$.
当AB的斜率存在时,设AB的斜率为k,则直线AB的方程为y-3=k(x-2),
代入圆的方程可得(1+k2)x2+(2-4k2)x+4k2-15=0,
∴x1+x2=$\frac{{4k}^{2}-2}{1{+k}^{2}}$,x1•x2=$\frac{{4k}^{2}-15}{1{+k}^{2}}$,
∴|x1-x2|=$\sqrt{{{(x}_{1}{+x}_{2})}^{2}-{4x}_{1}{•x}_{2}}$=2$\frac{\sqrt{7{k}^{2}+16}}{1+{k}^{2}}$.
∵△ABC的面积S=$\frac{1}{2}$•|CN|•|y1-y2|=3|k|•$\frac{\sqrt{7{k}^{2}+16}}{1+{k}^{2}}$,
令1+k2=t,(t≥1)则S2=9(-$\frac{9}{{t}^{2}}$+$\frac{2}{t}$+7),
当$\frac{1}{t}$=$\frac{1}{9}$即t=9,k=±2$\sqrt{2}$时,S2取得最大值64.
综上可得,△ABC的最大面积为8,此时直线AB的斜率为±2$\sqrt{2}$.
点评 本题主要考查直线和圆相切的性质,用点斜式求直线的方程,两个向量的数量积的运算,直线和圆的位置关系的综合应用,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<$\frac{1}{e}$ | B. | a>$\frac{1}{e}$ | C. | a>$\frac{1}{2}$ | D. | a<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
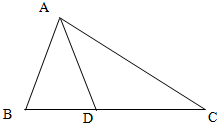 如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.
如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com