
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() ,在数列
,在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 是等比数列;
是等比数列;
(2)若![]() ,求数列
,求数列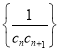 的前
的前![]() 项和
项和![]() ;
;
(3)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)利用递推关系可得![]() ,由等比数列的定义即可得出结论;(2)利用对数的运算性质可得
,由等比数列的定义即可得出结论;(2)利用对数的运算性质可得![]() ,根据裂项求和方法即可得出;(3)
,根据裂项求和方法即可得出;(3)![]() 时,
时, ![]() 时,
时, ![]() ,综上
,综上![]() ,可得
,可得![]() ,再利用错位相减法及分组求和法即可得结果.
,再利用错位相减法及分组求和法即可得结果.
试题解析:(1) 证明: ![]() 且
且![]()
![]()
![]() 是首项为4,公比为2的等比数列 .
是首项为4,公比为2的等比数列 .
(2) 由(1)知 ![]() ,
,
所以 ![]() ,
,
则![]()
![]() ,
,
![]()
![]() .
.
(3) ![]() 时
时 ![]() ,
,
![]() 时
时 ![]() ,
,
综上 ![]() ,
,
![]() ,解得
,解得
![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④![]()
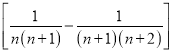 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】1979年,李政道博士给中国科技大学少年班出过一道智趣题:5只猴子分一堆桃子,怎么也不能分成5等份,只好先去睡觉,准备第二天再分,夜里1只猴子偷偷爬起来,先吃掉一个桃子,然后将其分成5等份,藏起自己的一份就去睡觉了;第2只猴子又爬起来,将剩余的桃子吃掉一个后,也将桃子分成5等份;藏起自己的一份睡觉去了;以后的3只猴子都先后照此办理,问:最初至少有多少个桃子?最后至少剩下多少个桃子?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率等于40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下2-组随机数:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每件一等品都能通过检测,每件二等品通过检测的概率为![]() .现有
.现有![]() 件产品,其中
件产品,其中![]() 件是一等品,
件是一等品, ![]() 件是二等品.
件是二等品.
(Ⅰ)随机选取![]() 件产品,设至少有一件通过检测为事件
件产品,设至少有一件通过检测为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(Ⅱ)随机选取![]() 件产品,其中一等品的件数记为
件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com