
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
| A. | 4<x≤9 | B. | 4≤x<9 | C. | x<4或x≥9 | D. | x≤4或x>9 |
分析 由随机变量ξ的分布列,知ξ2的可能取值为0,1,4,9,
分别求出相应的概率,由此利用P(ξ2<x)=$\frac{11}{12}$,求出实数x的取值范围.
解答 解:由随机变量ξ的分布列,知:
ξ2的可能取值为0,1,4,9,
且P(ξ2=0)=$\frac{4}{12}$,
P(ξ2=1)=$\frac{3}{12}$+$\frac{1}{12}$=$\frac{4}{12}$,
P(ξ2=4)=$\frac{1}{12}$+$\frac{2}{12}$=$\frac{3}{12}$,
P(ξ2=9)=$\frac{1}{12}$,
∵P(ξ2<x)=$\frac{11}{12}$,
∴实数x的取值范围是4<x≤9.
故选:A.
点评 本题考查了离散型随机变量的分布列性质的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
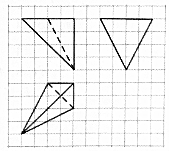 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{32}{3}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果不买彩票,那么就不能中奖,因为你买了彩票,所以你一定中奖 | |
| B. | 因为a>b,a>c,所以a-b>a-c | |
| C. | 若a,b均为正实数,则lga+lgb≥2$\sqrt{lga•lgb}$ | |
| D. | 若ab<0,则$\frac{a}{b}$+$\frac{b}{a}$=-[(-$\frac{a}{b}$)+(-$\frac{b}{a}$)]≤-2$\sqrt{(-\frac{a}{b})(-\frac{b}{a})}$≤-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com