Question

8．（理）把边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C-ABD，它的主视图与俯视图如图所示，则二面角C-AB-D的正切值为$\sqrt{2}$．

Answer 1

分析 根据三视图以及二面角的定义，作出二面角的平面角，利用三角形的边角关系进行求解即可．

解答 解：设折叠前C点的位置为C'，AC、BD的交点为O，
∵根据三视图，可得平面BCD⊥平面ABD，平面BCD∩平面ABD=BD且CO⊥BD
∴CO⊥平面ABD
∵OC'?平面ABD，∴CO⊥OC'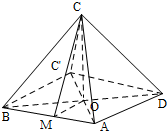
∵CO=C'O=$\frac{\sqrt{2}}{2}$，∴CC'=$\sqrt{O{C}^{2}+C'{O}^{2}}$=1=1，
取AB的中点M．连接OM，CM，
则OM⊥AB，CM⊥AB，
则∠CMA是二面角C-AB-D的平面角，
∵DC'=DC=1，
∴tan∠CMA=$\frac{OC}{OM}$$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=$\sqrt{2}$，
故答案为：$\sqrt{2}$

点评 本题主要考查二面角的求解，以及三视图的应用，利用定义法是解决本题的关键．