
 与
与 均为菱形,设
均为菱形,设 与
与 相交于点
相交于点 ,若
,若 ,且
,且 .
.
 ;
; 的余弦值.
的余弦值.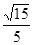 .
.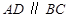 ,
,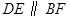 ,再根据线面平行的判定得
,再根据线面平行的判定得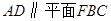 ,
,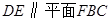 ,再根据面面平行的判定得面
,再根据面面平行的判定得面 面
面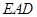 ,从而证明
,从而证明 ;第二问,先根据已知条件得建立空间直角坐标系的最基本的条件,即
;第二问,先根据已知条件得建立空间直角坐标系的最基本的条件,即 两两垂直,建立空间直角坐标系,写出点的坐标,求出平面
两两垂直,建立空间直角坐标系,写出点的坐标,求出平面 和平面
和平面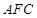 的法向量,利用夹角公式求出夹角并判断二面角为锐二面角,所以所求余弦值为正值.
的法向量,利用夹角公式求出夹角并判断二面角为锐二面角,所以所求余弦值为正值. 与
与 均为菱形,
均为菱形,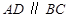 ,
,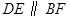 .
. ,
,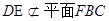 ,
,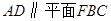 ,
,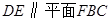 2分
2分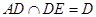 ,
,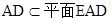 ,
,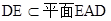 ,
,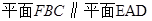
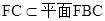 ,
, 4分
4分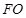 、
、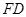 ,因为四边形
,因为四边形 为菱形,且
为菱形,且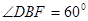 ,所以
,所以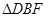 为等边三角形,
为等边三角形, 为
为 中点.所以
中点.所以 ,
, 为
为 中点,且
中点,且 ,
,
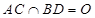 ,所以
,所以 .6分
.6分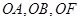 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系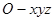
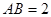 ,因为四边形
,因为四边形 为菱形,
为菱形,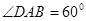 ,
,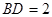 ,
,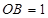 ,
,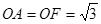 ,
,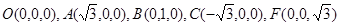 ..8分
..8分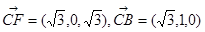 设平面
设平面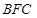 的一个法向量为
的一个法向量为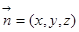 ,
,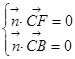 ,所以
,所以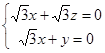 ,令
,令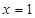 ,则
,则
 ,所以平面
,所以平面 的一个法向量为
的一个法向量为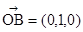 .10分
.10分 为锐二面角,设二面角的平面角为
为锐二面角,设二面角的平面角为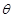
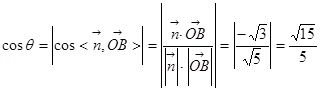
 的余弦值为
的余弦值为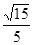 ..12分
..12分

科目:高中数学 来源:不详 题型:解答题
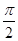 .
.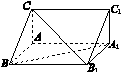
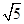 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
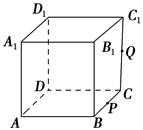
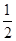 时,S为四边形;
时,S为四边形;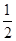 时,S为等腰梯形;
时,S为等腰梯形;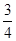 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;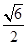 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,装的水恰好占其容积的一半;
,装的水恰好占其容积的一半; 表示水平的桌面,容器一边
表示水平的桌面,容器一边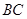 紧贴桌面,沿
紧贴桌面,沿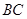 将其翻转使之倾斜,最后水面(阴影部分)与其各侧棱的交点分别是
将其翻转使之倾斜,最后水面(阴影部分)与其各侧棱的交点分别是 (如图),设翻转后容器中的水形成的几何体是
(如图),设翻转后容器中的水形成的几何体是 ,翻转过程中水和容器接触面积为
,翻转过程中水和容器接触面积为 ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 是棱柱, 是棱柱, 逐渐增大 逐渐增大 |
B. 是棱柱, 是棱柱, 始终不变 始终不变 |
C. 是棱台, 是棱台, 逐渐增大 逐渐增大 |
D. 是棱台, 是棱台, 始终不变 始终不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com