
| A. | 3 | B. | $\frac{3}{2}$+$\sqrt{2}$ | C. | 2+$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
分析 先求出圆心和半径,由直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-2y+1=0截得的弦长为2,可得直线ax-by+2=0经过圆心,可得a+b=2,代入式子再利用基本不等式可求式子的最小值.
解答 解:圆x2+y2+2x-2y+1=0 即 (x+1)2+(y-1)2=1,圆心为(-1,1),半径为1,
∵直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-2y+1=0截得的弦长为2,
∴直线ax-by+2=0经过圆心,∴-a-b+2=0,a+b=2,
则$\frac{1}{a}$+$\frac{2}{b}$=$\frac{1}{2}$(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=$\frac{1}{2}$(3+$\frac{b}{a}$+$\frac{2a}{b}$)≥$\frac{3}{2}+\sqrt{2}$,当且仅当$\sqrt{2}$a=b时等号成立,
故$\frac{1}{a}$+$\frac{2}{b}$的最小值为$\frac{3}{2}+\sqrt{2}$.
故选:B.
点评 本题考查直线和圆的位置关系,弦长公式以及基本不等式的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
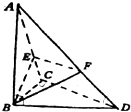 如图,在三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点.且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).
如图,在三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点.且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x,y∈R,且$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,则$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$ | |
| B. | △ABC中,A>B是sinA>sinB的充分必要条件 | |
| C. | 命题“若a=-1,则f(x)=ax2+2x-1只有一个零点”的逆命题为真 | |
| D. | 设命题p:?x>0,x2>2x,则¬p:?x0≤0,x02≤2x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某正三棱柱(底面是正三角形的直棱柱)的正视图和俯视图如图所示.若它的体积为2$\sqrt{3}$,则它的侧视图面积为( )
某正三棱柱(底面是正三角形的直棱柱)的正视图和俯视图如图所示.若它的体积为2$\sqrt{3}$,则它的侧视图面积为( )| A. | 2$\sqrt{3}$ | B. | 3 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com