
| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $\frac{1}{2}-\frac{π}{2}$ | C. | $\frac{1}{4}-\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
分析 根据平行线的距离公式求出满足条件.的直线对应的区域,求出对应的面积,利用几何概型的概率公式进行求解即可.
解答 解:设与直线x-y+2$\sqrt{2}$=0平行的直线方程为x-y+c=0,
若两平行直线的距离d=1,则d=$\frac{丨2\sqrt{2}-c丨}{\sqrt{2}}$=1,
解得c=$\sqrt{2}$或c=3$\sqrt{2}$,此时直线方程为x-y+$\sqrt{2}$=0或x-y+3$\sqrt{2}$=0,
圆心O,若两平行直线的距离d=3,则d=$\frac{丨2\sqrt{2}-c丨}{\sqrt{2}}$=3,
解得c=-$\sqrt{2}$或c=5$\sqrt{2}$,
∴直线方程为x-y-$\sqrt{2}$=0或x-y+5$\sqrt{2}$=0,
若满足到直线x-y+2$\sqrt{2}$=0的距离d∈[1,3]的点P,
则P对应的区域为阴影部分,
则第二象限,三角形OAB的面积S=$\frac{1}{2}$$\sqrt{2}$•$\sqrt{2}$=1,则第二象限内弓型的面积S=$\frac{1}{4}$•π($\sqrt{2}$)2-1=$\frac{π}{2}$-1,
则阴影部分的面积为2π-2($\frac{π}{2}$-1)=π+2,
则满足到直线x-y+2$\sqrt{2}$=0的距离d∈[1,3]的点P概率为$\frac{π+2}{2π}$=$\frac{1}{2}$+$\frac{π}{2}$,
故选A.
点评 本题主要考查几何概型的概率的计算,利用平行线的距离公式,结合对应区域的面积是解决本题的关键,属于中档题.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {0,1] | C. | {-1,0,1} | D. | N⊆{-2,-1,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)>f(3) | B. | f(2)>f(5) | C. | f(3)>f(5) | D. | f(3)>f(6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
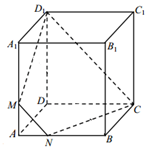 如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1
如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
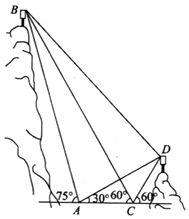 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com