Question

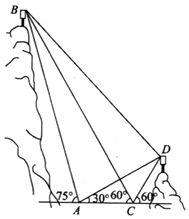
15．如图，A，B，C，D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶．测量船于水面A处测得B点和D点的仰角分别为75°，30°，于水面C处测得B点和D点的仰角均为60°，AC=1km．试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D间的距离．（计算结果精确到0.1km）参考数据：$\sqrt{2}≈1.41$，$\sqrt{6}$≈2.45．

Answer 1

分析 在△ACD中，∠DAC=30°推断出CD=AC，同时根据CB是△CAD底边AD的中垂线，判断出BD=BA，进而在△ABC中利用余弦定理求得AB答案可得．

解答 解：在△ACD中，∠DAC=30°，
∠ADC=60°-∠DAC=30°，
所以CD=AC=0.1．
又∠BCD=180-60°-60°=60°，
故CB是△CAD底边AD的中垂线，
所以BD=BA、
在△ABC中，AB=$\frac{ACsin60°}{sin15°}$=$\frac{3\sqrt{2}+\sqrt{6}}{20}$，
因此，BD=$\frac{3\sqrt{2}+\sqrt{6}}{20}$≈0.3km．
故B、D的距离约为0.3km．

点评 本题主要考查了解三角形的实际应用．考查学生分析问题解决问题的能力．综合运用基础知识的能力．