
分析 (1)由a3,m,S3成等比数列,得m2=a3•S3,由此能求出m的值.
(2)设等比数列{an}公比为q,由q=1和q≠1两种情况分类讨论,能求出首项.
解答 解:(1)因为a3,m,S3成等比数列,所以 m2=a3•S3…(1分)
因为${a_3}=\frac{3}{2}$,${S_3}=\frac{9}{2}$,所以 ${m^2}=\frac{27}{4}$…(2分)
所以$m=±\frac{{3\sqrt{3}}}{2}$…(4分)
(2)设等比数列{an}公比为q,
①当q=1时,${a_1}={a_2}={a_3}=\frac{3}{2}$,此时${S_3}=\frac{9}{2}$,满足题意,…(6分)
②当q≠1时,依题意得$\left\{\begin{array}{l}{a_1}{q^2}=\frac{3}{2}\\ \frac{{{a_1}(1-{q^3})}}{1-q}=\frac{9}{2}\end{array}\right.$…(8分)
解得$\left\{\begin{array}{l}{a_1}=6\\ q=\frac{1}{2}\end{array}\right.$,综上可得${a_1}=\frac{3}{2}$或a1=6.…(12分)
点评 本题考查实数值的求法,考查数列的首项的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房41017 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.3 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.3 | 4.4 | 4.1 | 4.2 | 4.3 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
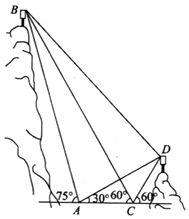 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
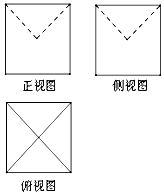 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com