
分析 首先画出三角函数式为最简形式,然后根据正弦函数的性质解之.
解答 解:由已知f(x)=(sinx+cosx)2+2cos2x=1+sin2x+cos2x+1=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+2,
所以(1)令2x+$\frac{π}{4}$∈[2kπ+$\frac{π}{2}$,2kπ$+\frac{3π}{2}$],得到f(x)的单调递减区间为[k$π+\frac{π}{8}$,k$π+\frac{5π}{8}$],k∈Z;
(2)$x∈[0,\frac{π}{2}]$时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],所以f(x)的值域为[1,2+$\sqrt{2}$];
(3)由$y=\sqrt{2}sinx$的任何一点的横坐标缩小为原来的$\frac{1}{2}$,纵坐标不变,然后向左平移$\frac{π}{8}$个单位,最后向上平移2个单位得到y=f(x)的图象.
点评 不同考查了三角函数式的化简以及利用正弦函数的性质解答关于正弦型函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
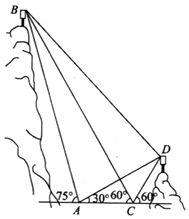 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com