
分析 (1)求导数,设切点,可得方程组,即可求切线l的方程;
(2)设f(x)=(x+1)ex,则f(x1)=f(x2).f'(x)=(x+2)ex,可得函数f(x)的单调性;设g(x)=f(x)-f(-4-x),切点其单调性,即可证明结论.
解答 (1)解:y'=ex,设切点(x0,y0),则$\left\{\begin{array}{l}{y_0}={e^{x_0}}\\{e^{x_0}}=\frac{y_0}{{{x_0}+1}}\end{array}\right.$,解得x0=0,
因此y'|x=0=1,l的方程是y=x+1.…(6分)
(2)证明:依题意有$\left\{\begin{array}{l}\frac{a}{{{e^{x_1}}}}={x_1}+1\\ \frac{a}{{{e^{x_2}}}}={x_2}+1\end{array}\right.$,所以$({x_1}+1){e^{x_1}}=({x_2}+1){e^{x_2}}$…(8分)
设f(x)=(x+1)ex,则f(x1)=f(x2).f'(x)=(x+2)ex,
当x<-2时,f'(x)<0,当x>-2时,f'(x)>0;
所以f(x)在(-∞,-2)单调递减,在(-2,+∞)单调递增.
因为x1≠x2,不妨设x1<-2,x2>-2.
设g(x)=f(x)-f(-4-x),则g'(x)=f'(x)+f'(-4-x)=(x+2)ex(1-e-2(2+x)),
当x>-2时,g'(x)>0,g(x)在在(-2,+∞)单调递增,
所以g(x)>g(-2)=0,所以当x>-2时,f(x)>f(-4-x).…(14分)
因为x2>-2,所以f(x2)>f(-4-x2),从而f(x1)>f(-4-x2),
因为-4-x2<-2,f(x)在(-∞,-2)单调递减,所以x1<-4-x2,即x1+x2<-4.…(16分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查不等式的证明,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
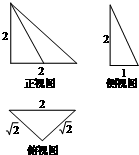 如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.
如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 第1列 | 第2列 | 第3列 | … | |
| 第1行 | 1 | 2 | 3 | … |
| 第2行 | 2 | 4 | 6 | … |
| 第3行 | 3 | 6 | 9 | … |
| … | … | … | … | … |
| A. | n2-n+1 | B. | n2-n | C. | n2+n | D. | n2+n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com