
分析 先求二次函数$y={x}^{2}-\frac{3}{2}x+1$在区间[$\frac{3}{4}$,2]上的值域,从而解出集合A,在解出集合B,根据“x∈A”是“x∈B”的充分条件即可得到关于m的不等式,从而解不等式即得实数m的取值范围.
解答 解:y=${x}^{2}-\frac{3}{2}x+1=(x-\frac{3}{4})^{2}+\frac{7}{16}$;
该函数在[$\frac{3}{4},2$]上单调递增,x=2时,y=2;
∴$A=\{y|\frac{7}{16}≤y≤2\}$,B={x|x≥1-m2};
∵x∈A是x∈B的充分条件;
∴$1-{m}^{2}≤\frac{7}{16}$;
解得m$≤-\frac{3}{4}$,或m$≥\frac{3}{4}$;
∴实数m的取值范围为$(-∞,-\frac{3}{4}]∪[\frac{3}{4},+∞)$.
点评 考查二次函数在闭区间上的值域的求法,描述法表示集合,以及充分条件的概念,解一元二次不等式.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
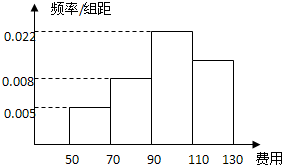 学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )| A. | 100 | B. | 120 | C. | 30 | D. | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com