
分析 把椭圆方程化为标准方程,求出左焦点F的坐标,然后利用待定系数法设出AB的方程,与椭圆的方程联立,消去y,得到关于x的一元二次方程,最后利用韦达定理、弦长公式求出直线的斜率,注意单独验证斜率不存在的情况.
解答 解:由椭圆3x2+4y2=48,得$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$,则a2=16,b2=12,
∴c=$\sqrt{{a}^{2}-{b}^{2}}=\sqrt{16-12}=2$,∴F(-2,0),
对于直线AB,
当AB⊥x轴时,将x=-2代入椭圆方程得y=±3,
∴|AB|=6,∴AB不垂直于x轴,
设直线AB方程为y=k(x+2),代入椭圆方程整理得:(3+4k2)x2+16k2x+16k2-48=0,
设A(x1,y1),B(x2,y2),
∴x1+x2=$\frac{-16{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{16{k}^{2}-48}{3+4{k}^{2}}$,
∴|AB|=$\sqrt{(1+{k}^{2})[(\frac{-16{k}^{2}}{3+4{k}^{2}})^{2}-\frac{64{k}^{2}-192}{3+4{k}^{2}}]}$=$\frac{24(1+{k}^{2})}{3+4{k}^{2}}=7$,
化简后得k2=$\frac{3}{4}$,∴k=±$\frac{\sqrt{3}}{2}$,
∴AB的方程为:$\sqrt{3}$x+2y+2$\sqrt{3}$=0或$\sqrt{3}$x-2y+2$\sqrt{3}$=0.
故答案为:$\sqrt{3}$x+2y+2$\sqrt{3}$=0或$\sqrt{3}$x-2y+2$\sqrt{3}$=0.
点评 本题考查了椭圆的标准方程及其性质以及直线与椭圆的位置关系,一般是将直线方程代入椭圆方程消去y(或x)的一元二次方程,然后进一步求解;本题是借助韦达定理、弦长公式构造出关于k的方程求解,计算量较大,是中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:解答题
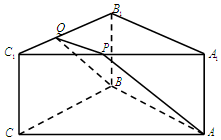 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$,0),($\sqrt{5}$,0) | B. | (0,-$\sqrt{5}$),(0,$\sqrt{5}$) | C. | (-$\sqrt{13}$,0),($\sqrt{13}$,0) | D. | (0,-$\sqrt{13}$),(0,$\sqrt{13}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
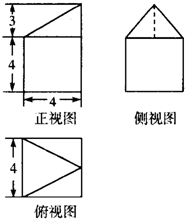
| A. | 98+6$\sqrt{5}$ | B. | 106+6$\sqrt{5}$ | C. | 114+6$\sqrt{5}$ | D. | 106+12$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2<m<4 | B. | -4<m<2 | C. | 2<m<4 | D. | -4<m<4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com