练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝loga|x|(a＞0且a≠1)在(－∞，0)上单调递增，则f(a＋1)与f(2)的大小关系为(　　)

    A．f(a＋1)＝f(2)                     B．f(a＋1)＞f(2)

    C．f(a＋1)＜f(2)                     D．不确定


    B

    [解析]　易知f(x)为偶函数，所以f(x)在(0，＋∞)上单调递减．所以0＜a＜1.则1＜a＋1＜2.所以f(a＋1)＞f(2)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知100件产品中有5件次品，从这100件产品任意取出3件，设A表示事件“3件产品全不是次品”，B表示事件“3件产品全是次品”，C表示事件“3件产品中至少有1件次品”，则下列结论正确的是(　　)

    A．B与C互斥

    B．A与C互斥

    C．A、B、C任意两个事件均互斥

    D．A、B、C任意两个事件均不互斥

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某人从甲地去乙地共走了500 m，途中要过一条宽为x m的河流，他不小心把一件物品丢在途中，若物品掉在河里就找不到，物品不掉在河里就能找到，已知该物品能被找到的概率为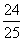，则河宽为(　　)

    A．16 m                              B．20 m

    C．8 m                               D．10 m

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    利用随机模拟方法主算如图中阴影部分(曲线y＝2x与x轴，x＝±1围成的部分)的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列各函数中，值域为(0，＋∞)的是(　　)

    A．y＝2－                          B．y＝

    C．y＝x2＋x＋1                        D．y＝3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝ax(a>0，a≠1)在[－1,2]上的最大值为4，最小值为m，且函数g(x)＝(1－4m)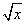在[0，＋∞)上是增函数，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    f(x)是定义在R上的函数，对x，y∈R都有f(x＋y)＝f(x)＋f(y)，且当x>0时，f(x)<0，f(－1)＝2.

    (1)求证：f(x)为奇函数；

    (2)求证：f(x)是R上的减函数；

    (3)求f(x)在[－2,4]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x2－2ax＋2，x∈[－3,3]．

    (1)当a＝－5时，求f(x)的最大值和最小值；

    (2)求实数a的取值范围，使y＝f(x)在区间[－3,3]上是单调函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将函数y＝log2x的图像上每一点的纵坐标不变，横坐标变为原来的m(m>0)倍，得到图像C，若将y＝log2x的图像向上平移2个单位，也得到图像C，则m＝________.

    查看答案和解析>>

    同步练习册答案