
f(x)是定义在R上的函数,对x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(-1)=2.
(1)求证:f(x)为奇函数;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在[-2,4]上的最值.
[解析] (1)f(x)的定义域为R,
令x=y=0,则f(0)=f(0)+f(0),
∴f(0)=0,
令y=-x,则f(x-x)=f(x)+f(-x),
∴f(-x)+f(x)=f(0)=0,
∴f(-x)=-f(x),
∴f(x)是奇函数.
(2)设x2>x1,
f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1),
∵x2-x1>0,∴f(x2-x1)<0,
∴f(x2)-f(x1)<0,
即f(x2)<f(x1),
∴f(x)在R上为减函数.
(3)∵f(-1)=2,
∴f(-2)=f(-1)+f(-1)=4,
∵f(x)为奇函数,
∴f(2)=-f(-2)=-4,
∴f(4)=f(2)+f(2)=-8,
∵f(x)在[-2,4]上为减函数,
∴f(x)max=f(-2)=4,
f(x)min=f(4)=-8.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
下列试验中,是古典概型的为( )
A.种下一粒花生,观察它是否发芽
B.向正方形ABCD内,任意投掷一点P,观察点P是否与正方形的中心O重合
C.从1、2、3、4四个数中,任取两个数,求所取两数之一是2的概率
D.在区间[0,5]内任取一点,求此点小于2的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
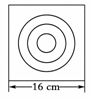 如图所示,在墙上挂着一块边长为16 cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2 cm,4 cm,6 cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,
如图所示,在墙上挂着一块边长为16 cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2 cm,4 cm,6 cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,
记事件A={投中大圆内},
事件B={投中小圆与中圆形成的圆环内},
事件C={投中大圆之外}.
(1)用计算机产生两组[0,1]内的均匀随机数,a1=RAND,b1=RNAD.
(2)经过伸缩和平移变换,a=16a1-8,b=16b1-8,得到两组[-8,8]内的均匀随机数.
(3)统计投在大圆内的次数N1(即满足a2+b2<36的点(a,b)的个数),投中小圆与中圆形成的圆环次数N2(即满足4<a2+b2<16的点(a,b)的个数),投中木板的总次数N(即满足上述-8<a<8,-8<b<8的点(a,b)的个数).
则概率P(A)、P(B)、P(C)的近似值分别是( )
A.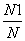 ,
,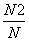 ,
,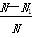 B.
B.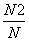 ,
,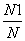 ,
,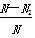
C.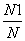 ,
,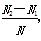 ,
,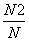 D.
D.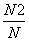 ,
,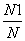 ,
,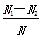
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=loga|x|(a>0且a≠1)在(-∞,0)上单调递增,则f(a+1)与f(2)的大小关系为( )
A.f(a+1)=f(2) B.f(a+1)>f(2)
C.f(a+1)<f(2) D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
在一次数学试验中,应用图形计算器采集到如下一组数据:
| x | -2.0 | -1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+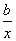
查看答案和解析>>
科目:高中数学 来源: 题型:
夏季高山温度从山脚起每升高100米,降低0.7摄氏度,已知山顶的温度是14.1摄氏度,山脚的温度是26摄氏度,则山的相对高度为( )
A.1750米 B.1730米
C.1700米 D.1680米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com