
若函数f(x)=ax(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)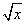 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为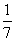 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是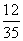 .则从中任意取出2粒恰好是同一色的概率是( )
.则从中任意取出2粒恰好是同一色的概率是( )
A.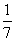 B.
B.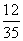
C. D.1
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=loga|x|(a>0且a≠1)在(-∞,0)上单调递增,则f(a+1)与f(2)的大小关系为( )
A.f(a+1)=f(2) B.f(a+1)>f(2)
C.f(a+1)<f(2) D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)在[a,b]上连续,且同时满足f(a)·f(b)<0,f(a)·f(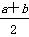 )>0.则( )
)>0.则( )
A.f(x)在[a,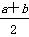 ]上有零点 B.f(x)在[
]上有零点 B.f(x)在[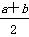 ,b]上有零点
,b]上有零点
C.f(x)在[a,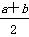 ]上无零点 D.f(x)在[
]上无零点 D.f(x)在[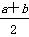 ,b]上无零点
,b]上无零点
查看答案和解析>>
科目:高中数学 来源: 题型:
某商品的市场日需求量Q1和日产量Q2均为价格P的函数,且Q1=144·(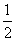 )P+12,Q2=6×2P,日总成本C关于日产量Q2的关系式为:
)P+12,Q2=6×2P,日总成本C关于日产量Q2的关系式为:
C=10+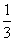 Q2.
Q2.
(1)Q1=Q2时的价格为均衡价格,求此均衡价格P0;
(2)当P=P0时,求日利润L的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com