练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝loga(1＋x)，g(x)＝loga(1－x)，(a＞0，a≠1)．

    (1)设a＝2，函数f(x)的定义域为[3,63]，求f(x)的最值；

    (2)求使f(x)－g(x)＞0的x的取值范围．


    [解析]　(1)当a＝2时，f(x)＝log2(1＋x)，

    在[3,63]上为增函数，因此当x＝3时，f(x)最小值为2.

    当x＝63时f(x)最大值为6.

    (2)f(x)－g(x)＞0即f(x)＞g(x)

    当a＞1时，loga(1＋x)＞loga(1－x)

    满足∴0＜x＜1

    当0＜a＜1时，loga(1＋x)＞loga(1－x)

    满足∴－1<x＜0

    综上a＞1时，解集为{x|0＜x＜1}

    0＜a＜1时解集为{x|－1<x＜0}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.

    一次购物量

    1至4件

    5至8件

    9至12件

    13至16件

    17件及以上

    顾客数(人)

    x

    30

    25

    y

    10

    结算时间

    (分钟/人)

    1

    1.5

    2

    2.5

    3

    已知这100位顾客中的一次购物量超过8件的顾客占55%.

    (1)确定x，y的值，并估计顾客一次购物的结算时间的平均值．

    (2)求一位顾客一次购物的结算时间不超过2分钟的概率．(将频率视为概率)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设x是[0,1]内的一个均匀随机数，经过变换y＝2x＋3，则x＝对应变换成的均匀随机数是(　　)

    A．0                                 B．2

    C．4                                 D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝1＋log2x与g(x)＝21－x在同一直角坐标系下的图象大致是(　　)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝ax(a>0，a≠1)在[－1,2]上的最大值为4，最小值为m，且函数g(x)＝(1－4m)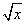在[0，＋∞)上是增函数，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(x)＝x3(x∈R)，则函数y＝－f(－x)在其定义域上是(　　)

    A．递减的偶函数                        B．递增的偶函数

    C．递减的奇函数                        D．递增的奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝－4x2＋4ax－4a－a2(a<0)在区间[0,1]上有最大值－5，则实数a等于(　　)

    A．－1                                 B．－

    C．－                                D．－5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二次函数f(x)＝ax2＋bx＋c(x∈R)的部分对应值如下表：

    x

    －3

    －2

    －1

    0

    1

    2

    3

    4

    y

    6

    m

    －4

    －6

    －6

    －4

    n

    6

    由此可以判断方程ax2＋bx＋c＝0的两个根所在的区间是(　　)

    A．(－3，－1)和(2,4)                 B．(－3，－1)和(－1,1)

    C．(－1,1)和(1,2)                    D．(－∞，－3)和(4，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)的图像如图所示，则函数f(x)的零点个数为(　　)

    A．1                                   B．2

    C．3                                   D．4

    查看答案和解析>>

    同步练习册答案