
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间 (分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并估计顾客一次购物的结算时间的平均值.
(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
(1)由已知得,
25+y+10=55,x+y=35,
所以x=15,y=20,
该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为一个容量为100的简单随机样本,顾客一次购物的结算时间的平均值可用样本平均数估计,其估计值为:
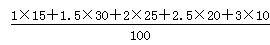 =1.9(分钟).
=1.9(分钟).
(2)记A为事件“一位顾客一次购物的结算时间不超过2分钟”,A1、A2、A3分别表示事件“该顾客一次购物的结算时间为1分钟”、“该顾客一次购物的结算时间为1.5分钟”、“该顾客一次购物的结算时间为2分钟”.将频率视为概率,得
P(A1)=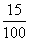 =
= ,P(A2)=
,P(A2)=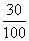 =
=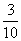 ,
,
P(A3)= =
=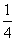 .
.
因为A=A1∪A2∪A3,且A1,A2,A3是互斥事件,
所以P(A)=P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)= +
+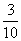 +
+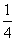 =
=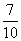 .
.
故一位顾客一次购物的结算时间不超过2分钟的概率为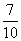 .
.


科目:高中数学 来源: 题型:
从存放号码分别为1,2,…,10的卡片的盒子里,有放回地取100次,每次取一张卡片,并记下号码,统计结果如下:
| 卡片号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 取到的次数 | 13 | 8 | 5 | 7 | 6 | 13 | 18 | 10 | 11 | 9 |
则取到号码为奇数的频率是( )
A.0.53 B.0.5
C.0.47 D.0.37
查看答案和解析>>
科目:高中数学 来源: 题型:
某种彩票的抽奖是从写在36个球上的36个号码中随机摇出7个.有人统计了过去中特等奖的号码,声称某一号码在历次特等奖中出现的次数最多,它是一个幸运号码,人们应该买这一号码;也有人说,若一个号码在历次特等奖中出现的次数最少,由于每个号码出现的机会相等,应该买这一号码,你认为他们的说法对吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为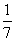 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是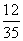 .则从中任意取出2粒恰好是同一色的概率是( )
.则从中任意取出2粒恰好是同一色的概率是( )
A.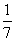 B.
B.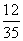
C. D.1
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率为( )
A.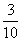 B.
B.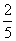
C.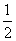 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中有五张卡片,其中红色卡片三张,标号分别为1、2、3;蓝色卡片两张,标号分别为1、2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在一个边长为a、b(a>b>0)的矩形内画一个梯形,梯形上、下底边分别为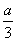 与
与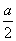 ,高为b.向该矩形内随机地投一点,则所投的点落在梯形内部的概率为( )
,高为b.向该矩形内随机地投一点,则所投的点落在梯形内部的概率为( )
A.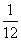 B.
B.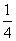 C.
C.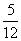 D.
D.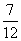
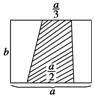
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com