
若f(x)=x3(x∈R),则函数y=-f(-x)在其定义域上是( )
A.递减的偶函数 B.递增的偶函数
C.递减的奇函数 D.递增的奇函数
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率为( )
A.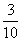 B.
B.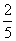
C.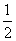 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
利用随机模拟方法计算y=x2与y=4围成的面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1·4-2,b=b1·4,试验进行100次,前98次中落在所求面积区域内的样本点数为65,已知最后两次试验的随机数a1=0.3,b1=0.8及a1=0.4,b1=0.3,那么本次模拟得出的面积约为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)是定义在[-6,6]上的偶函数,且在[-6,0]上单调递减,则( )
A.f(3)+f(4)<0 B.f(-3)-f(-2)<0
C.f(-2)+f(-5)<0 D.f(4)-f(-1)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
“龟兔赛跑”讲过了这样一个故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到了终点,用S1、S2分别表示乌龟和兔子所行的路线,t为时间,则图中与故事情节相吻合的是( )
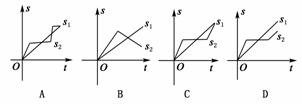
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x.则函数g(x)=f(x)-x+3的零点的集合为( )
A.{1,3} B.{-3,-1,1,3}
C.{2-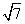 ,1,3} D.{-2-
,1,3} D.{-2-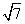 ,1,3}
,1,3}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com