
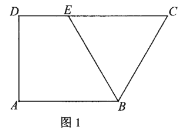
【题目】图1是直角梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .以
.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.
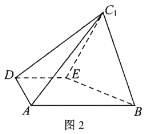
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点O为极点,
),以原点O为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知![]() ,曲线
,曲线![]() 与
与![]() 的交点A, B满足
的交点A, B满足![]() (A为第一象限的点),求
(A为第一象限的点),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的右焦点为F,离心率为
1(a>b>0)的右焦点为F,离心率为![]() ,且有3a2=4b2+1.
,且有3a2=4b2+1.
(1)求椭圆C的标准方程;
(2)过点F的直线l与椭圆C交于M,N两点,过点M作直线x=3的垂线,垂足为点P,证明直线NP经过定点,并求出这个定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() :
:![]() .给出以下四个命题:
.给出以下四个命题:
①分别过点![]() ,
,![]() ,作
,作![]() 的不同于
的不同于![]() 轴的切线,两切线相交于点
轴的切线,两切线相交于点![]() ,则点
,则点![]() 的轨迹为椭圆的一部分;
的轨迹为椭圆的一部分;
②若![]() ,
,![]() 相切于点
相切于点![]() ,则点
,则点![]() 的轨迹恒在定圆上;
的轨迹恒在定圆上;
③若![]() ,
,![]() 相离,且
相离,且![]() ,则与
,则与![]() ,
,![]() 都外切的圆的圆心在定椭圆上;
都外切的圆的圆心在定椭圆上;
④若![]() ,
,![]() 相交,且
相交,且![]() ,则与
,则与![]() ,
,![]() 一个内切一个外切的圆的圆心的轨迹为椭圆的一部分.
一个内切一个外切的圆的圆心的轨迹为椭圆的一部分.
则以上命题正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 长轴长为4,右焦点
长轴长为4,右焦点![]() 到左顶点的距离为3.
到左顶点的距离为3.
(1)求椭圆![]() 的方程;
的方程;
(2)设过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点(
两点(![]() 不在坐标轴上),连接
不在坐标轴上),连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点,且交椭圆于A,B两点,线段AB的中点是
的右焦点,且交椭圆于A,B两点,线段AB的中点是![]() ,
,
(1)求椭圆的方程;
(2)过原点的直线l与线段AB相交(不含端点)且交椭圆于C,D两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在创建“全国卫生文明城”的过程中,环保部门对某市市民进行了一次垃圾分类知识的网络问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(Ⅰ)已知此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求![]() ;
;
(Ⅱ)在(Ⅰ)的条件下,环保部门为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次赠送的随机话费和相应的概率如下表.现市民甲要参加此次问卷调查,记![]() 为该市民参加问卷调查获赠的话费,求
为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
赠送的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com