
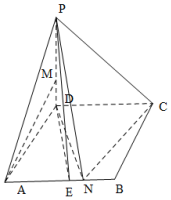
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,分析 (Ⅰ)在PC上去一点F,使PF=2FC,连接MF,NF,证明FM∥DC,AN∥DC,推出$MF\stackrel{∥}{=}AN$.得到AM∥NA
然后证明直线AM∥平面PNC.
(Ⅱ)证明CD⊥DE.CD⊥PD,利用直线与平面垂直的判定定理证明CD⊥平面PDE.
(Ⅲ)说明DE为点A到平面PDC的距离,求出底面面积,利用等体积法求解几何体的体积即可.
解答 (本小题共14分)
证明:(Ⅰ)在PC上去一点F,使PF=2FC,连接MF,NF,因为PM=2MD,AN=2NB,所以FM∥DC,$MF=\frac{2}{3}DC$,AN∥DC,AN=$\frac{2}{3}AB=\frac{2}{3}DC$,
所以$MF\stackrel{∥}{=}AN$.
所以MFNA为平行四边形
即AM∥NA
又AM?平面PNC
所以直线AM∥平面PNC….(5分)
(Ⅱ)因为E是AB中点,底面ABCD是菱形,∠DAB=60°,所以∠AED=90°
因为AB∥CD,所以,∠EDC=90°即CD⊥DE.
又PD⊥平面ABCD,所以CD⊥PD
又DE∩PD=D所以直线CD⊥平面PDE…(11分)
(Ⅲ)直线AB∥DC,且由(Ⅱ)可知,DE为点A到平面PDC的距离,${S_{△PDC}}=\frac{1}{2}PD•DC=\frac{9}{2}$,$DE=\frac{{3\sqrt{3}}}{2}$,${V_{C-PDA}}={V_{A-PDC}}=\frac{1}{3}{S_{△PDC}}•DE=\frac{{9\sqrt{3}}}{4}$.….(14分)
点评 本题考查直线与平面垂直的判定定理与直线与平面平行的判定定理的应用,几何体的体积的求法,考查转化思想以及空间想象能力计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(α)>f(β)>f(γ) | B. | f(α)>f(γ)>f(β) | C. | f(β)>f(α)>f(γ) | D. | f(β)>f(γ)>f(α) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={x^{\frac{1}{2}}}-1$ | B. | f(x)=2x-1 | C. | $f(x)=ln({x-\frac{1}{3}})$ | D. | f(x)=2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,2] | B. | [-3,2) | C. | [1,2] | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com