
设函数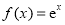 (
(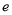 为自然对数的底数),
为自然对数的底数),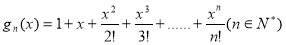
(1)证明: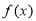
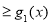 ;
;
(2)当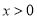 时,比较
时,比较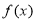 与
与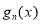 的大小,并说明理由;
的大小,并说明理由;
(3)证明: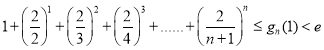 (
(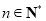 ).
).
试题分析:(1)构造函数Φ(x)=f(x)-g1(x),证明Φ(x)的最小值非负即可;(2)结合(1),利用数学归纳法,可以证明f(x)>gn(x);(3)先证 ,再叠加,然后由(2)得
,再叠加,然后由(2)得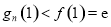 即可.
即可.
试题解析:(1)见解析;(2)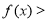
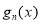 ;(3)见解析.
;(3)见解析.
【解析】(1)证明:设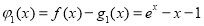 ,所以
,所以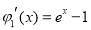
当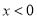 时,
时,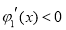 ,当
,当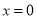 时,
时, ,当
,当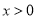 时,
时,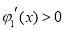 .
.
即函数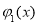 在
在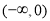 上单调递减,在
上单调递减,在 上单调递增,在
上单调递增,在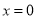 处取得唯一极小值
处取得唯一极小值
因为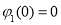 ,所以对任意实数
,所以对任意实数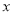 均有
均有 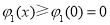 .即
.即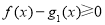 ,
,
所以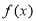
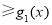 4分
4分
(2)【解析】
当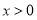 时,
时,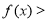
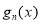 .用数学归纳法证明如下:
.用数学归纳法证明如下:
①当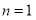 时,由(1)知
时,由(1)知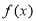
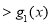 .
.
②假设当 (
(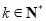 )时,对任意
)时,对任意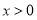 均有
均有
 ,
,
令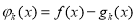 ,
,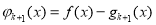 ,
,
因为对任意的正实数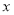 ,
, ,
,
由归纳假设知,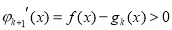 .
.
即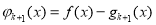 在
在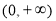 上为增函数,亦即
上为增函数,亦即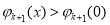 ,
,
因为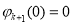 ,所以
,所以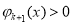 .从而对任意
.从而对任意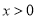 ,有
,有 .
.
即对任意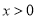 ,有
,有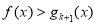 .这就是说,当
.这就是说,当 时,对任意
时,对任意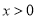 ,也有
,也有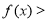
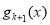 .由①、②知,当
.由①、②知,当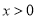 时,都有
时,都有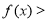
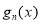 .
.
(3)证明1:先证对任意正整数 ,
,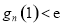 .
.
由(2)知,当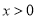 时,对任意正整数
时,对任意正整数 ,都有
,都有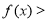
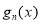 .令
.令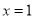 ,得
,得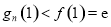 .所以
.所以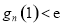 .再证对任意正整数
.再证对任意正整数 ,
,
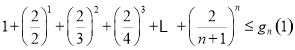
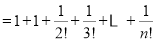 .
.
要证明上式,只需证明对任意正整数 ,不等式
,不等式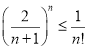 成立.
成立.
即要证明对任意正整数 ,不等式
,不等式 (*)成立 10分
(*)成立 10分
以下分别用数学归纳法和基本不等式法证明不等式
①当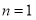 时,
时, 成立,所以不等式(*)成立.
成立,所以不等式(*)成立.
②假设当 (
(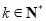 )时,不等式(*)成立,即
)时,不等式(*)成立,即 . 11分
. 11分
则 .
.
因为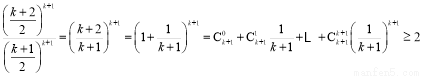
所以 . 13分
. 13分
这说明当 时,不等式(*)也成立.由①、②知对任意正整数
时,不等式(*)也成立.由①、②知对任意正整数 ,不等式(*)都成立.
,不等式(*)都成立.
综上可知,对任意正整数 ,
,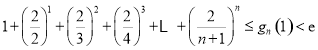 成立 14分
成立 14分
考点:利用导数研究函数的性质,不等式,数列求和


科目:高中数学 来源: 题型:
|
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 4 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
已知x,y∈(0,1),且 lnx,
lnx, ,lny成等比数列,则xy有( )
,lny成等比数列,则xy有( )
A.最小值e B.最小值 C.最大值e D.最大值
C.最大值e D.最大值
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
已知复数z1=cos23°+isin23°和复数z2=cos37°+isin37°,则z1•z2为( )
A.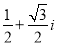 B.
B.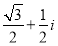 C.
C.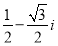 D.
D.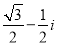
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:解答题
已知函数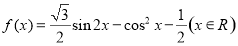
(1)当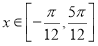 时,求函数f(x)取得最大值和最小值时
时,求函数f(x)取得最大值和最小值时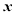 的值;
的值;
(2)设锐角△ABC的内角A、B、C的对应边分别是a,b,c,且a=1,c∈N*,若向量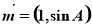 与向量
与向量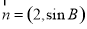 平行,求c的值.
平行,求c的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:选择题
设函数 ,其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-
,其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-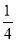 x-
x-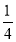 不同零点的个数为( )
不同零点的个数为( )
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com