Question

1．如图所示的“数阵”的特点是：毎行每列都成等差数列，则数字37在图中出现的次数为9．

Answer 1

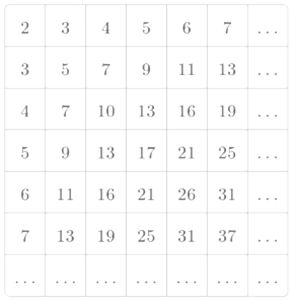
分析 第1行数组成的数列A1j（j=1，2，…）是以2为首项，公差为1的等差数列，第j列数组成的数列Aij（i=1，2，…）是以j+1为首项，公差为j的等差数列，求出通项公式，就求出结果

解答 解：第i行第j列的数记为Aij．那么每一组i与j的组合就是表中一个数．
因为第一行数组成的数列A1j（j=1，2，…）是以2为首项，公差为1的等差数列，
所以A1j=2+（j-1）×1=j+1，
所以第j列数组成的数列Aij（i=1，2，…）是以j+1为首项，公差为j的等差数列，
所以Aij=（j+1）+（i-1）×j=ij+1．
令Aij=ij+1=37，
则ij=36=2²×3²，
∴37出现的次数为（2+1）（2+1）=9，
故答案为：9．

点评 本题考查了行列模型的等差数列应用，解题时利用首项和公差写出等差数列的通项公式，运用通项公式求值，是中档题