
分析 (1)根据参数方程和极坐标方程和普通方程的关系进行转化即可;
(2)将直线方程代入圆的方程得到关于t的二次方程,根据判别式求出关于m的方程,解出即可.
解答 解:(1)M的直角坐标为(3,3),
圆C的直角坐标方程为(x-1)2+y2=4,
设直线l:y-3=k(x-3),即l:kx-y-3k+3=0,
因为直线l与圆C相切,所以$\frac{|2k-3|}{{\sqrt{{k^2}+1}}}=2$,解得$k=\frac{5}{12}$,
此时直线l的方程为5x-12y+21=0,
若直线l的斜率不存在时,直线l的方程为x=3,
所以直线l的极坐标方程为5ρcosθ-12ρsinθ+21=0或ρcosθ=3.
(2)将直线l'的参数方程$\left\{{\begin{array}{l}{x=\frac{1}{2}t}\\{y=m+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数),
代入圆C的方程(x-1)2+y2=4,
得:t2+($\sqrt{3}$m-1)t+m2-3=0,
$△={(\sqrt{3}m-1)^2}-4({m^2}-3)$=$-{m^2}-2\sqrt{3}m+13>0$,
设PA=t1,PB=t2,则${t_1}•{t_2}={m^2}-3$,
因为|PA|•|PB|=6,所以$|{t_1}•{t_2}|=|{m^2}-3|=6$,
所以m2-3=±6,解得m=±3,
由△>0知,所求m的值为-3.
点评 本题考查了参数方程和极坐标方程以及普通方程的关系,考查二次函数的性质,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
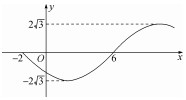 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | 4π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 | 患流感 | 未患流感 |
| 服用药 | 2 | 18 |
| 未服用药 | 8 | 12 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.05 | B. | 0.025 | C. | 0.01 | D. | 0.005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com