
分析 (1)求出集合C={x|x≥0},则B∩C,B∪C的答案可求;
(2)由题意列出不等式组,求解得到$x≥\frac{1-m}{2}$,又A⊆C,则$\frac{1-m}{2}≥0$,求出m的范围即可得到实数m的最大值.
解答 解:(1)集合B={x|-3<x<2},C={x|2x-1≥0}={x|x≥0}.
则B∩C={x|-3<x<2}∩{x|x≥0}={x|0≤x<2},
B∪C={x|-3<x<2}∪{x|x≥0}={x|x>-3};
(2)由题意知$\left\{\begin{array}{l}{lo{g}_{2}(2x+m)≥0}\\{2x+m>0}\end{array}\right.$,
解得:2x+m≥1即$x≥\frac{1-m}{2}$.
又A⊆C,∴$\frac{1-m}{2}≥0$.
∴m≤1.
∴实数m的最大值为1.
点评 本题考查了交集、并集及其运算,考查了函数的定义域及其求法,考查了对数函数的性质,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{{D_1}{B_1}}$ | B. | $\overrightarrow{{D_1}B}$ | C. | $\overrightarrow{D{B_1}}$ | D. | $\overrightarrow{B{D_1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x>2,则x2+x≤6 | B. | 若x2+x≤6,则x≤2 | C. | 若x2+x<6,则x<2 | D. | 若x≤2,则x2+x≤6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
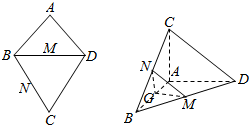 如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
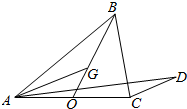 如图,在△ABC中,BO为边AC上的中线,$\overrightarrow{BG}=2\overrightarrow{GO}$,设$\overrightarrow{CD}$∥$\overrightarrow{AG}$,若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$(λ∈R),则λ的值为( )
如图,在△ABC中,BO为边AC上的中线,$\overrightarrow{BG}=2\overrightarrow{GO}$,设$\overrightarrow{CD}$∥$\overrightarrow{AG}$,若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$(λ∈R),则λ的值为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{6}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com