
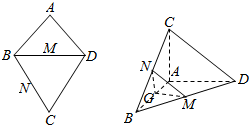
 如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.分析 (Ⅰ)利用线面平行的判定定理,证明MN∥平面ADC′,NG∥平面ADC,再利用面面平行的判定定理证明平面GNM∥平面ADC′;
(Ⅱ)利用AD⊥平面C′AB,证明AD⊥C′A,利用勾股定理的逆定理,证明AB⊥C′A,再利用线面垂直的判定定理证明C′A⊥平面ABD.
解答 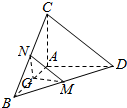 (本题满分为10分)
(本题满分为10分)
解:(Ⅰ)因为M,N分别是BD,BC′的中点,
所以MN∥DC′.
因为MN?平面ADC′,
DC′?平面ADC′,所以MN∥平面ADC′.
同理NG∥平面ADC′.
又因为MN∩NG=N,
所以平面GNM∥平面ADC′…(5分)
(Ⅱ)因为∠BAD=90°,所以AD⊥AB.
又因为AD⊥C′B,且AB∩C′B=B,所以AD⊥平面C′AB.
因为C′A?平面C′AB,所以AD⊥C′A.
因为△BCD是等边三角形,AB=AD,
不妨设AB=1,则BC=CD=BD=$\sqrt{2}$,可得C′A=1.
由勾股定理的逆定理,可得AB⊥C′A.
因为AB∩AD=A,
所以C′A⊥平面ABD…(10分)
点评 本题主要考查了面面平行,线面垂直的判定,考查了学生分析解决问题的能力、空间想象能力和推理论证能力,正确运用面面平行、线面垂直的判定定理是解题的关键,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com