
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\sqrt{3}$ |
分析 正方体ABCD-A1B1C1D1的外接球球心O为对角线AC1的中点,球半径$R=\sqrt{3}$,球心O到平面EFG的距离为$\frac{{2\sqrt{3}}}{3}$,利用勾股定理求出小圆半径.
解答 解:由题意,正方体ABCD-A1B1C1D1的外接球球心O为对角线AC1的中点,正方体对角线长为2$\sqrt{3}$
所以球半径$R=\sqrt{3}$,
因为A到平面EFG的距离为$\frac{\sqrt{3}}{3}$
所以球心O到平面EFG的距离为$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{{2\sqrt{3}}}{3}$,
所以小圆半径$r=\sqrt{{R^2}-{{({\frac{{2\sqrt{3}}}{3}})}^2}}=\frac{{\sqrt{15}}}{3}$,
故选B.
点评 本题考查平面EFG截球O所得圆的半径及球的内接多面体问题,找准量化关系是关键.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{6}$ | B. | 向左平移$\frac{π}{6}$ | C. | 向左平移$\frac{π}{3}$ | D. | 向右平移$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
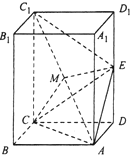 如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,M为AC1的中点,连结C1E,CE,AC,AE,ME,CM.
如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,M为AC1的中点,连结C1E,CE,AC,AE,ME,CM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
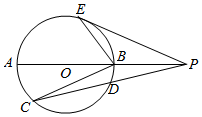 如图,半径为2的⊙O的直径AB的延长线与弦CD的延长线相交与点P,PE为⊙O的切线,E为切点,$\overrightarrow{BE}$=2$\overrightarrow{BD}$,若PB=2,PD=$\frac{5}{2}$,∠PEB=30°.
如图,半径为2的⊙O的直径AB的延长线与弦CD的延长线相交与点P,PE为⊙O的切线,E为切点,$\overrightarrow{BE}$=2$\overrightarrow{BD}$,若PB=2,PD=$\frac{5}{2}$,∠PEB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2017) | B. | (0,2018) | C. | (2017,+∞) | D. | (2018,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com