
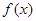 的定义域为
的定义域为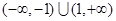 ,对定义域内的任意x,满足
,对定义域内的任意x,满足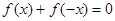 ,当
,当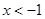 时,
时,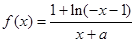 (a为常),且
(a为常),且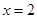 是函数
是函数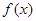 的一个极值点,
的一个极值点,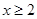 时,不等式
时,不等式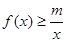 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;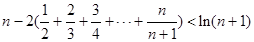
 ;(2)2;(3)详见解析.
;(2)2;(3)详见解析.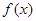 为奇函数,所以设
为奇函数,所以设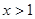 ,利用
,利用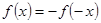 ,求出
,求出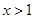 时的
时的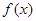 ,然后再求
,然后再求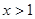 时的
时的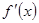 ,再根据
,再根据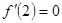 ,求出
,求出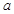 ,验证所求
,验证所求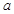 能够使
能够使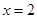 是函数
是函数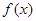 的一个极值点;(2)不等式
的一个极值点;(2)不等式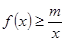 恒成立,转化为
恒成立,转化为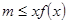 恒成立,设
恒成立,设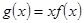 ,即求
,即求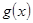 的最小值,求
的最小值,求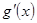
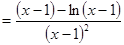 ,再设
,再设 ,易求
,易求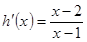 ,当
,当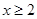 时,
时,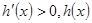 为增函数,
为增函数,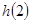 最小,
最小,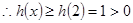 ,即
,即 逐步分析
逐步分析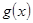 为单调递增函数,从而求得最小值.(3)通过
为单调递增函数,从而求得最小值.(3)通过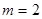 代入(2)式恒成立不等式
代入(2)式恒成立不等式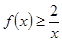 ,变形放缩后得到
,变形放缩后得到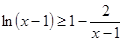 ,为出现(2)要证形式,所以令
,为出现(2)要证形式,所以令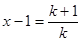 ,则
,则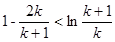 ,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.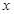 ,
,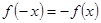 ,
,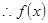 为奇函数,
为奇函数,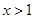 时,
时,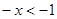 ,
,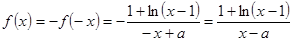 ,
,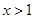 时,
时,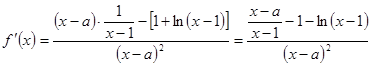
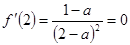 ,解得
,解得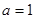 ,经验证,满足题意.
,经验证,满足题意.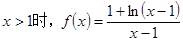
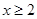 时,
时,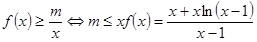 ,令
,令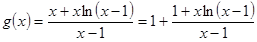
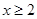 时,
时,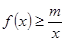 恒成立,转化为
恒成立,转化为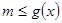 在
在 恒成立.
恒成立.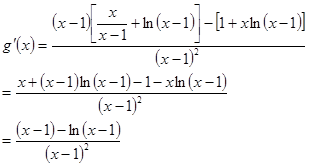
 ,
,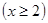 ,则
,则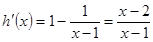 ,
,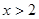 时,
时,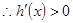 ,
,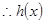 在
在 上单调递增.
上单调递增.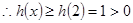
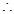 当
当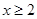 时,
时,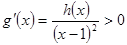 ,
,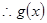 在
在 单调递增.
单调递增.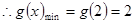
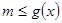 在
在 恒成立,则
恒成立,则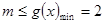
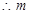 的最大值2.
的最大值2.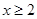 时,有
时,有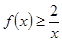 ,即
,即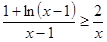
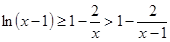
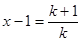 ,则
,则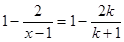
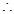 当
当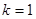 时,
时,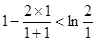 ;当
;当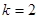 时,
时, ;当
;当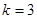 时,
时,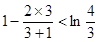 ;
;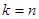 时,
时,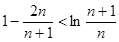
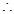 将以上不等式两端分别相加得:
将以上不等式两端分别相加得:
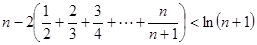 .
.

科目:高中数学 来源:不详 题型:单选题
| A.(-∞,-1) | B.(-∞,2 -1) -1) |
C.(-1,2 -1) -1) | D.(-2 -1,2 -1,2 -1) -1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是定义在
是定义在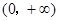 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记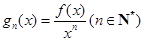 .若对定义域内的每一个
.若对定义域内的每一个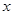 ,总有
,总有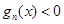 ,则称
,则称 为“
为“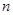 阶负函数 ”;若对定义域内的每一个
阶负函数 ”;若对定义域内的每一个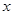 ,总有
,总有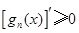 ,则称
,则称 为“
为“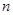 阶不减函数”(
阶不减函数”(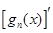 为函数
为函数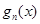 的导函数).
的导函数).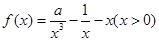 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数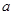 的取值范围;
的取值范围; ,如果存在常数
,如果存在常数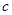 ,使得
,使得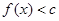 恒成立,试判断
恒成立,试判断 是否为“2阶负函数”?并说明理由.
是否为“2阶负函数”?并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com