
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对于①,可通过举f(x)=x3,可得f(x)在x=0处的导数为0,但f(x)在R上递增,无极值.结合极值和充分必要条件的定义即可判断;
对于②,运用全称命题的否定为特称命题,注意量词的变化和不等号的变化,即可判断;
对于③,运用逆命题与否命题等价,即可判断.
解答 解:对于①,对于定义域内的可导函数f(x),f(x)在某处的导数为0,
比如f(x)=x3,f′(x)=3x2≥0,由f(x)在x=0处的导数为0,但f(x)在R上递增,无极值;
反之,若f(x)在某点处取到极值,则由极值的定义可得f(x)在某处的导数为0,
故f(x)在某处的导数为0是f(x)在该处取到极值的必要不充分条件,则①正确;
对于②,命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0>1”,则②错误;
对于③,若一个命题的逆命题为真,由互为逆否命题等价,则它的否命题一定为真,则③错误.
其中不正确的个数为2.
故选:C.
点评 本题考查命题的真假判断和应用,主要是充分必要条件的判断和命题的否定,以及四种命题和等价命题的判断,考查导数的运用:求极值,考查判断能力,属于基础题和易错题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
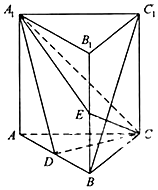 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 8 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},3}]$ | B. | $[{\frac{1}{2},3})$ | C. | (-∞,3] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com