
分析 把已知等式移向平方,整理后再移向平方,化简得答案.
解答 解:由$\sqrt{(x-5)^{2}+{y}^{2}}$-$\sqrt{(x+5)^{2}+{y}^{2}}$=6,得:
$\sqrt{(x-5)^{2}+{y}^{2}}$=$\sqrt{(x+5)^{2}+{y}^{2}}$+6,两边平方得:
${x}^{2}-10x+25+{y}^{2}={x}^{2}+10x+25+{y}^{2}+12\sqrt{(x+5)^{2}+{y}^{2}}+36$,
即$3\sqrt{(x+5)^{2}+{y}^{2}}=-5x-9$,两边再平方得:
$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$,由题意可知,其中x≤-3.
故答案为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$(x≤-3).
点评 本题考查根式与分数指数幂的互化及其化简运算,考查了计算能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | f(-$\frac{1}{2}$)>f($\frac{\sqrt{3}}{2}$) | B. | f($\frac{1}{3}$)<f(-$\frac{1}{2}$) | C. | f($\frac{1}{2}$)<f($\frac{\sqrt{3}}{2}$) | D. | f(-$\frac{1}{4}$)<f(-$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
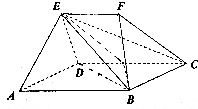 如图所示,在多面体ABCDEF中,面ABCD是平行四边形,EF∥AB,EF:AB=1:2,则四棱锥E-ABCD与三棱锥E-BCF的体积比为4.
如图所示,在多面体ABCDEF中,面ABCD是平行四边形,EF∥AB,EF:AB=1:2,则四棱锥E-ABCD与三棱锥E-BCF的体积比为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com