
分析 (1)根据x的范围即可求出x+1的范围(0,1),而f(x)的值域为(0,+∞),从而根据对数函数的单调性便可得出a∈(0,1);
(2)分离常数即可得到$g(x)=1-\frac{2}{{a}^{x}+1}$,这样根据a∈(0,1),以及x>0即可得到0<ax<1,根据不等式的性质即可求出g(x)的值域.
解答 解:(1)∵x∈(-1,0);
∴x+1∈(0,1);
又loga(x+1)∈(0,+∞);
∴0<a<1;
即a的取值范围为(0,1);
(2)$g(x)=\frac{{a}^{x}-1}{{a}^{x}+1}=1-\frac{2}{{a}^{x}+1}$;
∵0<a<1,x>0;
∴0<ax<1;
∴$1<\frac{2}{{a}^{x}+1}<2$;
∴$-1<1-\frac{2}{{a}^{x}+1}<0$;
∴该函数的值域为(-1,0).
点评 考查函数定义域、值域的概念及求法,对数函数的图象及单调性,指数函数的图象及单调性,分离常数法的运用,以及不等式的性质.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{15}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “φ=$\frac{π}{2}$”是“函数y=sin(2x+ϕ)为偶函数”的充要条件 | |
| B. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| C. | 命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | |
| D. | 当a<0时,幂函数y=xa在(0,+∞)上是单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
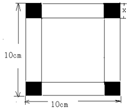 边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.
边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com