
分析 (1)根据两向量垂直数量积为0,列出方程求出k的值;
(2)利用向量的共线定理,列出方程求出k的值.
解答 解:(1)因为$(\overrightarrow a+k\overrightarrow b)⊥(\overrightarrow a-k\overrightarrow b)$,
所以$(\overrightarrow a+k\overrightarrow b)(\overrightarrow a-k\overrightarrow b)=0$,
所以${\overrightarrow a^2}-{k^2}{\overrightarrow b^2}=0$,…(3分)
因为$|{\overrightarrow a}|=3$,$|{\overrightarrow b}|=4$,
所以9-16k2=0,
解得$k=±\frac{3}{4}$;
(2)因为$(k\overrightarrow a-4\overrightarrow b)$∥$(\overrightarrow a-k\overrightarrow b)$,且$\overrightarrow a-k\overrightarrow b≠0$,
所以存在实数λ,使得$k\overrightarrow a-4\overrightarrow b=λ(\overrightarrow a-k\overrightarrow b)=λ\overrightarrow a-λk\overrightarrow b$,
因为$|{\overrightarrow a}|=3$,$|{\overrightarrow b}|=4$,且$\overrightarrow a$与$\overrightarrow b$不共线,
所以$\left\{\begin{array}{l}k=λ\\-4=-kπ\end{array}\right.$,
解得k=±2.
点评 本题考查了向量垂直于共线的应用问题,也考查了方程思想的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}})$ | B. | $({-1,\frac{1}{2}})$ | C. | $({0,\frac{1}{2}})$ | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
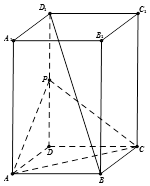 .如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
.如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com