
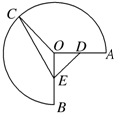
 如图,半径为1,圆心角为$\frac{3π}{2}$的圆弧$\widehat{AB}$上有一点C.
如图,半径为1,圆心角为$\frac{3π}{2}$的圆弧$\widehat{AB}$上有一点C.分析 (1)以O为原点,以OA为x轴正方向,建立图示坐标系,设D(t,0)(0≤t≤1),求出C坐标,推出$\overrightarrow{OC}+\overrightarrow{OD}=(t-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$,然后求出模的最小值.
(2)设C(cosθ,sinθ),$θ∈[0,\frac{3}{2}π]$,求出$\overrightarrow{CE}$•$\overrightarrow{CD}$的表达式,即可求出$\overrightarrow{CE}$•$\overrightarrow{CD}$的取值范围.
解答 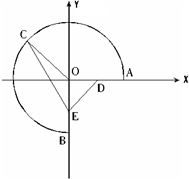 解:(1)以O为原点,OA为x轴建立直角坐标系,则$A(1,0),B(0,-1),C(-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$
解:(1)以O为原点,OA为x轴建立直角坐标系,则$A(1,0),B(0,-1),C(-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$
设D(t,0)(0≤t≤1),则$\overrightarrow{OC}+\overrightarrow{OD}=(t-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$,
所以$|\overrightarrow{OC}+\overrightarrow{OD}|=\sqrt{{{(t-\frac{{\sqrt{2}}}{2})}^2}+{{(\frac{{\sqrt{2}}}{2})}^2}}$,
当$t=\frac{{\sqrt{2}}}{2}$时,$|\overrightarrow{OC}+\overrightarrow{OD}{|_{min}}=\frac{{\sqrt{2}}}{2}$.
(2)由题意$D(\frac{1}{2},0),E(0,-\frac{1}{2})$,设C(cosθ,sinθ),$θ∈[0,\frac{3}{2}π]$
所以$\overrightarrow{CE}•\overrightarrow{CD}=(cosθ-\frac{1}{2},sinθ)(cosθ,sinθ+\frac{1}{2})=1+\frac{1}{2}sinθ-\frac{1}{2}cosθ$=$\frac{{\sqrt{2}}}{2}sin(θ-\frac{π}{4})+1$.
因为$θ∈[0,\frac{3}{2}π]$,则$sin(θ-\frac{π}{4})∈[-\frac{1}{2},\frac{{\sqrt{2}}}{2}]$,所以$\overrightarrow{CE}•\overrightarrow{CD}∈[\frac{1}{2},1+\frac{{\sqrt{2}}}{2}]$.
点评 本题考查向量的数量积,向量的表示方法,三角运算,考查转化思想,计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
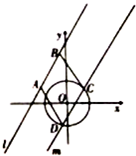 如图,已知直线l:y=$\sqrt{3}$x+4,圆O:x2+y2=3,直线m∥l.
如图,已知直线l:y=$\sqrt{3}$x+4,圆O:x2+y2=3,直线m∥l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com