
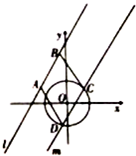
 如图,已知直线l:y=$\sqrt{3}$x+4,圆O:x2+y2=3,直线m∥l.
如图,已知直线l:y=$\sqrt{3}$x+4,圆O:x2+y2=3,直线m∥l.分析 (1)利用m∥l,求出直线l;设直线m的方程,利用设圆心O到直线m的距离为d,通过直线m与圆O相交,求解即可.
(2)求出CD,利用AB与CD之间的距离,结合$h=\frac{{\sqrt{3}}}{2}|{CD}|$求解即可.
解答 解:(1)∵m∥l,直线$l:y=\sqrt{3}x+4$,
∴可设直线$m:y=\sqrt{3}x+b$,即$\sqrt{3}x-y+b=0$,
设圆心O到直线m的距离为d,又因为直线m与圆O相交,
∴$d=\frac{|b|}{{\sqrt{{{({\sqrt{3}})}^2}+{{({-1})}^2}}}}<r=\sqrt{3}$,…(2分)
即$-2\sqrt{3}<b<2\sqrt{3}$,∴$b∈({-2\sqrt{3},2\sqrt{3}})$…(4分)
(2)由$|{CD}|=2\sqrt{{r^2}-{d^2}}=2\sqrt{3-\frac{b^2}{4}}$,①…(6分)
AB与CD之间的距离$h=\frac{{|{b-4}|}}{2}$,②…(8分)
又$h=\frac{{\sqrt{3}}}{2}|{CD}|$③…(10分)
联立①②③得到:b2-2b-5=0,又$b∈({-2\sqrt{3},2\sqrt{3}})$,
解得:$b=1+\sqrt{6}$或$b=1-\sqrt{6}$…(12分)
点评 本题考查直线与圆的位置关系的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,弦AE交BC于D,已知AD2=BD•DC,∠ADC=60°,OD=1,OE⊥BC.
如图,△ABC内接于⊙O,弦AE交BC于D,已知AD2=BD•DC,∠ADC=60°,OD=1,OE⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
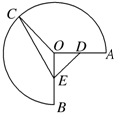 如图,半径为1,圆心角为$\frac{3π}{2}$的圆弧$\widehat{AB}$上有一点C.
如图,半径为1,圆心角为$\frac{3π}{2}$的圆弧$\widehat{AB}$上有一点C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k∈[-$\frac{3}{4}$,0) | B. | k∈(0,$\frac{4}{3}$] | C. | k∈(0,$\frac{3}{4}$] | D. | k∈[-$\frac{3}{4}$,$\frac{3}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1588 | B. | 0.1587 | C. | 0.1586 | D. | 0.1585 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2Sn=an+1 | B. | Sn=2an+1 | C. | 2Sn=an-1 | D. | Sn=2an-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com