
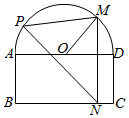
 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.分析 (1)设MN交AD交于Q点由∠MOD=30°,利用锐角三角函数可求MQ,OQ,进而可求MN,AQ,代入S△PMN=$\frac{1}{2}$MN•AQ可求;
(2)设∠MOQ=θ,由θ∈[0,$\frac{π}{2}$],结合锐角三角函数的定义可求MQ=sinθ,OQ=cosθ,代入三角形的面积公式S△PMN=$\frac{1}{2}$MN•AQ=$\frac{1}{2}$(1+sinθ)(1+cosθ)展开利用换元法,转化为二次函数的最值求解.
解答 解:(1)设MN交AD交于Q点,
∵PM=PN,
∴点P在线段AB上,
∵∠MQD=30°,
∴MQ=1,OQ=$\sqrt{3}$
∴S△PMN=$\frac{1}{2}$MN•AQ=$\frac{1}{2}$×3×(2+$\sqrt{3}$)=$\frac{{6+3\sqrt{3}}}{2}$….…(7分)
(2)设∠MOD=θ$({θ∈[{0,\frac{π}{2}}]})$,则 MQ=2sinθ,OQ=2cosθ.
设P到MN的距离为h,则h≤|AQ|=2+2cosθ,
∴S△PMN=$\frac{1}{2}$MN•h≤$\frac{1}{2}$(2+2sinθ)(2+2cosθ)=2 (1+sinθcosθ+sinθ+cosθ)
令sinθ+cosθ=t∈$[{1,\sqrt{2}}]$,则S△PMN=2 (1+$\frac{{{t^2}-1}}{2}$+t)=(t+1)2
当t=$\sqrt{2}$即θ=$\frac{π}{4}$,且P在线段AB上时,S△PMN取得最大值,最大值为$3+2\sqrt{2}$.…(15分)
点评 本题主要考查了三角函数的定义的应用及利用三角函数求解函数的最值,换元法的应用是求解的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | bn>cn | B. | bn<cn | C. | bn≥cn | D. | bn≤cn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | $6\sqrt{3}$ | C. | 6 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14π}{3}$ | B. | $-\frac{14π}{3}$ | C. | $\frac{7π}{18}$ | D. | $-\frac{7π}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com