
分析 (1)利用等比中项可${{a}_{3}}^{2}$=a1•a9,结合a1=2解方程可知公差d=2,进而计算可得结论;
(2)通过(1)裂项可知$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{2n•({2n+2})}}=\frac{1}{4}({\frac{1}{n}-\frac{1}{n+1}})$,进而并项相加即得结论.
解答 解:(1)∵a3是a1,a9的等比中项,{an}是等比数列,
∴${{a}_{3}}^{2}$=a1•a9,即$({a}_{1}+2d)^{2}$=a1(a1+8d),
又∵a1=2,
∴(2+2d)2=2•(2+8d),
化简得:d2-2d=0,
又∵d≠0,
∴d=2,
∴an=2n;
(2)由(1)可知$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{2n•({2n+2})}}=\frac{1}{4}({\frac{1}{n}-\frac{1}{n+1}})$,
∴${T_n}=\frac{1}{4}({1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…\frac{1}{n}-\frac{1}{n+1}})=\frac{1}{4}({1-\frac{1}{n+1}})=\frac{n}{{4({n+1})}}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
| X | 0 | 1 |
| P | 0.1 | 0.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=kπ+(-1)k•$\frac{π}{6}$,k∈Z | B. | x=2kπ+(-1)k•$\frac{π}{6}$,k∈Z | ||
| C. | x=kπ+(-1)k+1•$\frac{π}{6}$,k∈Z | D. | x=2kπ+(-1)k+1•$\frac{π}{6}$,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
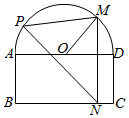 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com