
已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
(1)因为a1+a2+…+an-pan+1=0,所以n≥2时,a1+a2+…+an-1-pan=0,两式相减,得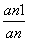 =
=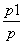 (n≥2),故数列{an}从第二项起是公比为
(n≥2),故数列{an}从第二项起是公比为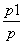 的等比数列,又当n=1时,a1-pa2=0,解得a2=
的等比数列,又当n=1时,a1-pa2=0,解得a2=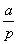 ,
,
从而an=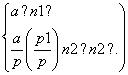
(2)①由(1)得ak+1=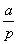
 k-1,
k-1,
ak+2=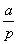
 k,ak+3=
k,ak+3=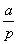
 k+1,
k+1,
若ak+1为等差中项,则2ak+1=ak+2+ak+3,
即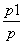 =1或
=1或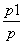 =-2,解得p=-
=-2,解得p=-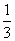 ;
;
此时ak+1=-3a(-2)k-1,ak+2=-3a(-2)k,
所以dk=|ak+1-ak+2|=9a·2k-1,
若ak+2为等差中项,则2ak+2=ak+1+ak+3,
即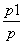 =1,此时无解;
=1,此时无解;
若ak+3为等差中项,则2ak+3=ak+1+ak+2,
即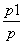 =1或
=1或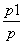 =-
=-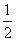 ,解得p=-
,解得p=-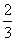 ,
,
此时ak+1=-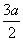
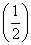 k-1,ak+3=-
k-1,ak+3=-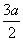
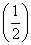 k+1,
k+1,
所以dk=|ak+1-ak+3|=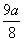 ·
·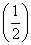 k-1,
k-1,
综上所述,p=-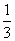 ,dk=9a·2k-1或p=-
,dk=9a·2k-1或p=-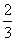 ,
,
dk=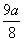 ·
·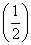 k-1.
k-1.
②当p=-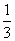 时,Sk=9a(2k-1).
时,Sk=9a(2k-1).
则由Sk<30,得a< ,
,
当k≥3时, <1,所以必定有a<1,
<1,所以必定有a<1,
所以不存在这样的最大正整数.
当p=-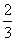 时,Sk=
时,Sk=
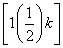 ,
,
则由Sk<30,得a<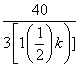 ,因为
,因为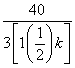 >
>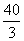 ,所以a=13满足Sk<30恒成立;但当a=14时,存在k=5,使得a>
,所以a=13满足Sk<30恒成立;但当a=14时,存在k=5,使得a>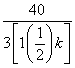 即Sk<30,
即Sk<30,
所以此时满足题意的最大正整数a=13.


科目:高中数学 来源: 题型:
如图是一个半圆形湖面景点的平面示意图.已知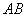 为直径,且
为直径,且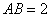 km,
km, 为圆心,
为圆心,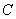 为圆周上靠近
为圆周上靠近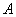 的一点,
的一点,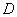 为圆周上靠近
为圆周上靠近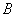 的一点,且
的一点,且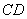 ∥
∥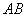 .现在准备从
.现在准备从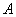 经过
经过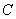 到
到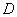 建造一条观光路线,其中
建造一条观光路线,其中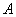 到
到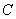 是圆弧
是圆弧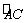 ,
,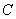 到
到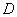 是线段
是线段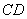 .设
.设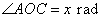 ,观光路线总长为
,观光路线总长为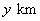 .
.
(1)求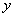 关于
关于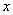 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
某学生在校举行的环保知识大奖赛中,答对每道题的概率都是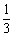 , 答错每道题的概率都是
, 答错每道题的概率都是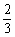 ,答对一道题积5分,答错一道题积-5分,答完n道题后的总积分记为
,答对一道题积5分,答错一道题积-5分,答完n道题后的总积分记为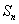 .
.
(1)答完2道题后,求同时满足S1=5且 的概率;
的概率;
(2)答完5道题后,设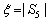 ,求
,求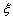 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知极坐标系的极点与直角坐标系的原点重合,极轴与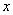 轴的正半轴重合.若直线
轴的正半轴重合.若直线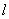 的极坐标方程为
的极坐标方程为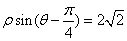 .
.
(1)把直线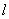 的极坐标方程化为直角坐标系方程;
的极坐标方程化为直角坐标系方程;
(2)已知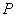 为椭圆
为椭圆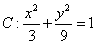 上一点,求
上一点,求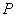 到直线
到直线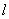 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com