某学生在校举行的环保知识大奖赛中，答对每道题的概率都是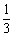
, 答错每道题的概率都是
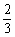,答对一道题积5分,答错一道题积-5分,答完n道题后的总积分记为
.
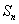（1）答完2道题后,求同时满足S1=5且
的概率；
（2）答完5道题后,设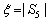
，求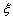
的分布列及其数学期望.
阅读快车系列答案科目：高中数学 来源： 题型：
已知数列{an}满足a1＝a(a＞0，a∈N*)，a1＋a2＋…＋an－pan＋1＝0(p≠0，p≠－1，n∈N*)．
(1)求数列{an}的通项公式an；
(2)若对每一个正整数k，若将ak＋1，ak＋2，ak＋3按从小到大的顺序排列后，此三项均能构成等差数列，且公差为dk.①求p的值及对应的数列{dk}．
②记Sk为数列{dk}的前k项和，问是否存在a，使得Sk＜30对任意正整数k恒成立？若存在，求出a的最大值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
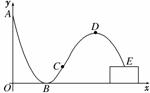
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动．如图，助跑道ABC是一段抛物线，某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1 m的平台上E处，飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内)，D为这段抛物线的最高点．现在运动员的滑行轮迹所在平面上建立如图所示的直角坐标系，x轴在地面上，助跑道一端点A(0,4)，另一端点C(3,1)，点B(2,0)，单位：m.
(1)求助跑道所在的抛物线方程；
(2)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线，为使运动员安全和空中姿态优美，要求运动员的飞行距离在4 m到6 m之间(包括4 m和6 m)，试求运动员飞行过程中距离平台最大高度的取值范围．
(注：飞行距离指点C与点E的水平距离，即这两点横坐标差的绝对值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
题，第一题答对，第二题答错；或第一题答对，第二题也答对” 
． 
道，此时
，
；答对
道，此时
，
；
；答对
道，此时
；
道，此时
；答对
道，此时
， 
，
，
的分布列为：
在
处取得最值的概率是 .
满足：
.
在矩阵
，求曲线
在点
处的切线方程为________． 
＝{1,2,3,4,5}，
＝{2,4}，则
＝ ．