
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |
分析 由已知AF2⊥F1F2,A(c,$\frac{{a}^{2}}{{b}^{2}}$),直线AB的方程是y=$\frac{\sqrt{2}}{2}$x,联立$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,得:a2b2=a4-2b4,由此能求出椭圆的离心率.
解答 解:∵$\overrightarrow{A{F}_{2}}$$•\overrightarrow{{F}_{1}{F}_{2}}$=0,∴AF2⊥F1F2,
设A(c,y),则$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,∴y=$\frac{{a}^{2}}{{b}^{2}}$,
又∵A,B是椭圆上的两点,且满足$\overrightarrow{OA}$$+\overrightarrow{OB}$=$\overrightarrow{0}$(O为坐标原点),
∴A,B关于原点对称,
∵直线AB的斜率为$\frac{\sqrt{2}}{2}$,
∴直线AB的方程是y=$\frac{\sqrt{2}}{2}$x,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,得${x}^{2}=\frac{{a}^{2}{b}^{2}}{\frac{1}{2}{a}^{2}+{b}^{2}}$=c2=a2-b2,
整理,得:a2b2=a4-2b4,
∴a2(a2-c2)=a4-2(a2-c2)2,
整理,得2a4-5a2c2+2c4=0,
∴2e4-5e+2=0,
解得e2=$\frac{1}{2}$或e2=2(舍),
又0<e<1,∴e=$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意椭圆性质、直线方程等知识点的合理运用.


科目:高中数学 来源: 题型:解答题
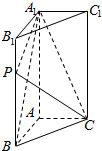 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
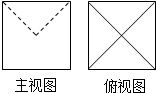 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )| A. | 24 | B. | 20+4$\sqrt{2}$ | C. | 24+4$\sqrt{2}$ | D. | 20+4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ESLE后面的语句不可以是条件语句 | |
| B. | 两个条件语句可以共用一个END IF语句 | |
| C. | 条件语句可以没有ELSE后的语句 | |
| D. | 条件语句中IF-THEN语句和ELSE后的语句必须同时存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | -$\frac{π}{4}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7-4$\sqrt{3}$ | B. | 5-2$\sqrt{6}$ | C. | 9-6$\sqrt{2}$ | D. | 8-2$\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com