练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

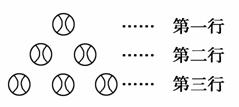
    数字1,2,3,4,5,6按如图形式随机排列，设第一行这个数为N1，N2、N3分别表示第二、三行中的最大数，则满足N1<N2<N3的所有排列的个数是________．


    240

    [解析]　由题意知6必在第三行，安排6有C种方法，第三行中剩下的两个空位安排数字有A种方法，在留下的三个数字中，必有一个最大数，把这个最大数安排在第二行，有C种方法，剩下的两个数字有A种排法，按分步计数原理，所有排列的个数是C×A×C×A＝240.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    袋中共有6个除了颜色外完全相同的球，其中有1个红球，2个白球和3个黑球．从袋中任取两球，两球颜色为一白一黑的概率等于(　　)

    A.                                                              B. 

    C.                                                              D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    袋内装有6个球，这些球依次被编号为1、2、3、…、6，设编号为n的球重n2－6n＋12(单位：g)，这些球等可能地从袋里取出(不受重量、编号的影响)．

    (1)从袋中任意取出一个球，求其重量大于其编号的概率；

    (2)如果不放回地任意取出2个球，求它们重量相等的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某单位有7个连在一起的车位，现有3辆不同型号的车需停放，如果要求剩余的4个车位连在一起，则不同的停放方法的种数为(　　)

    A．16                                                           B．18 

    C．24                                                           D．32

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某农科院在3行3列9块试验田中选出3块种植某品种水稻进行试验，则每行每列都有一块试验田种植水稻的概率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    6位同学安排到3个社区A，B，C参加志愿者服务，每个社区安排两名同学，其中甲同学必须到A社区，乙和丙同学均不能到C社区，则不同的安排方法种数为(　　)

    A．12　　 　                                                 B．9　　　　

    C．6　　　　                                                 D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一条街道上共有12盏路灯，为节约用电又不影响照明，决定每天晚上十点熄灭其中的4盏，并且不能熄灭相邻两盏也不能熄灭两头两盏，问不同熄灯方法有多少种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}的第5项是二项式(－)6展开式的常数项，则a3a7＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某学校数学兴趣小组有10名学生，其中有4名女学生；英语兴趣小组有5名学生，其中有3名女学生，现采用分层抽样方法，从数学兴趣小组、英语兴趣小组中共抽取3名学生参加科技节活动．

    (1)求从数学兴趣小组、英语兴趣小组各抽取的人数；

    (2)求从数学兴趣小组抽取的学生中恰有1名女学生的概率；

    (3)记ξ表示抽取的3名学生中男学生数，求ξ的分布列及数学期望．

    查看答案和解析>>

    同步练习册答案