
一条街道上共有12盏路灯,为节约用电又不影响照明,决定每天晚上十点熄灭其中的4盏,并且不能熄灭相邻两盏也不能熄灭两头两盏,问不同熄灯方法有多少种.
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
先后抛掷两枚均匀的正方体骰子(他们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x、y,则log2xy=1的概率为( )
A.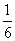 B.
B.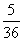
C. D.
D.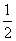
查看答案和解析>>
科目:高中数学 来源: 题型:
数字1,2,3,4,5,6按如图形式随机排列,设第一行这个数为N1,N2、N3分别表示第二、三行中的最大数,则满足N1<N2<N3的所有排列的个数是________.
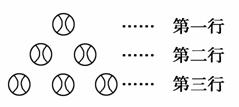
查看答案和解析>>
科目:高中数学 来源: 题型:
某班班会准备从含甲、乙的7名学生中选取4人发言,要求甲、乙2人至少有一人参加,若甲、乙同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序种数为( )
A.720 B.520
C.600 D.360
查看答案和解析>>
科目:高中数学 来源: 题型:
在(1+x)5+(1+x)6+(1+x)7的展开式中,含x4项的系数是首项为-2,公差为3的等差数列的( )
A.第11项 B.第13项
C.第18项 D.第20项
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com