
���� ��������Բ�Ľ�����x���ϣ���b=1��������Բ�������ʹ�ʽ���������a��ֵ�����������Բ�ķ��̣�
������ֱ��l�ķ��̣�������Բ���̣�����Τ�ﶨ�����е����깫ʽ�����M�����꣬����ֱ�ߵ�б�ʹ�ʽ���������k��ֵ�����ֱ��l�ķ��̣�
��� �⣺��������Բ��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����a=$\sqrt{2}$c��b2=a2-c2=c2��
����Բ�Ľ�����x���ϣ���P��0��1������Բ��һ�㣬
��b=1��c2=1��a2=2��
����Բ�ı����̣�$\frac{{x}^{2}}{2}+{y}^{2}=1$��
�����ɣ���֪F��1��0������ֱ��AB�ķ��̣�y=k��x-1������k��0����A��x1��y1����B��x2��y2����M��x0��y0����
$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���������1+2k2��x2-4k2x+2k2-2=0��
x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$��x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$��
��y1+y2=k��x1-1��+k��x2-1��=-$\frac{2k}{1+2{k}^{2}}$��x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{2{k}^{2}}{1+2{k}^{2}}$��y0=$\frac{{y}_{1}+{y}_{2}}{2}$=-$\frac{k}{1+2{k}^{2}}$��
��M��$\frac{2{k}^{2}}{1+2{k}^{2}}$��-$\frac{k}{1+2{k}^{2}}$����
��ֱ��OM��б��kOM=-$\frac{{y}_{0}}{{x}_{0}}$=-$\frac{1}{2k}$=-$\frac{1}{2}$����ã�k=1��
��ֱ��l�ķ��̣�x-y-1=0��
���� ���⿼����Բ�ı����̼��������ʣ�ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����е����깫ʽ��Ӧ�ã�������������������е��⣮


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
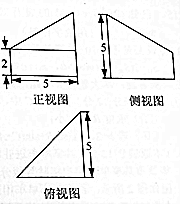 ���������������й��Ŵ���һ����ѧר���������й��ڡ�ǵ�¡��ļ��أ���ǵ�¡���������ֱ�������ε�ֱ����������֪ij��ǵ�¡���һ��ƽ���ȥһ���ֺ�ʣ�²��ֵ�����ͼ��ͼ��ʾ����ʣ�²��ֵ�����ǣ�������
���������������й��Ŵ���һ����ѧר���������й��ڡ�ǵ�¡��ļ��أ���ǵ�¡���������ֱ�������ε�ֱ����������֪ij��ǵ�¡���һ��ƽ���ȥһ���ֺ�ʣ�²��ֵ�����ͼ��ͼ��ʾ����ʣ�²��ֵ�����ǣ�������| A�� | 50 | B�� | 75 | C�� | 25.5 | D�� | 37.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1+3i | B�� | -1-3i | C�� | 1+3i | D�� | 1-3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | 31��12��22��15��20��45��47��32��34��23��28 |
| A�� | 23��32 | B�� | 34��35 | C�� | 28��32 | D�� | 28��35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a���ܱ�2017���� | B�� | b���ܱ�2017���� | ||
| C�� | a��b�����ܱ�2017���� | D�� | a��b��������һ���ܱ�2017���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 81 | B�� | 243 | C�� | 729 | D�� | 2187 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com