
 ��ͼ�����ֳ��е�Ħ����������ת��ÿתһȦ��Ҫ12���ӣ�����Բ��O�������40.5�ף��뾶40�ף���������ʹ�����Ħ���֣���ô�������ľ��뽫��ʱ��ı仯���仯���������Ħ���ֵ�ʱ�̿�ʼ��ʱ�������������⣮
��ͼ�����ֳ��е�Ħ����������ת��ÿתһȦ��Ҫ12���ӣ�����Բ��O�������40.5�ף��뾶40�ף���������ʹ�����Ħ���֣���ô�������ľ��뽫��ʱ��ı仯���仯���������Ħ���ֵ�ʱ�̿�ʼ��ʱ�������������⣮ ���� ��1�����������֪Ӧ���������ͺ���ģ�ͽ��⣬��Ħ���ֵ�ת������Ϊ12���ӣ����Ϊ40��������ú�������ʽ��
��2����40.5-40cos$\frac{��}{6}$t=60.5���Ӷ��õ�$\frac{��}{6}$t=2k��+$\frac{2}{3}��$��2k��+$\frac{4}{3}��$��k��N����$\frac{��}{6}$t=2��+$\frac{4}{3}��$�����t=20�����ӣ���
��3����������ϵ�����㵽���P�������ѵ����Q��ֻ��PQ�͵���ʱ�����������������ľ���֮������������t=2�����ӣ���������ΪPQ=40���ף���
��� �⣺��1������֪����y=40.5-40cos��t��t��0������Ϊ12���ӿ�֪��
��t=6ʱ��Ħ���ֵ�һ�ε�����ߵ㣬��������һ��ȡ�����ֵ������6��=�У�����=$\frac{��}{6}$��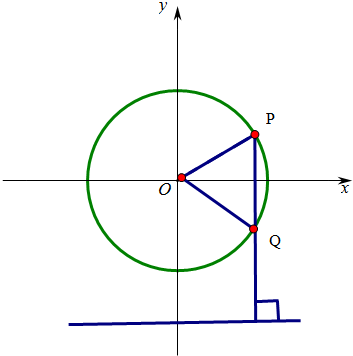
����y=40.5-40cos$\frac{��}{6}$t��t��0
��2����40.5-40cos$\frac{��}{6}$t=60.5����cos$\frac{��}{6}$t=$\frac{1}{2}$����$\frac{��}{6}$t=2k��+$\frac{2}{3}��$��2k��+$\frac{4}{3}��$��k��N
�ʵ�����Ĵξ������60.5��ʱ��k=1����$\frac{��}{6}$t=2��+$\frac{4}{3}��$�����t=20�����ӣ�
��3��������ͼ����ϵ�����㵽���P�������ѵ����Q��ֻ��PQ�͵���ʱ�����������������ľ���֮�����
��ͼ����֪������ת��$\frac{��}{3}$ʱ����Ҫ��$\frac{��}{6}$t=$\frac{��}{3}$����t=2�����ӣ���
������Ϊ��PQ=r=40���ף�
�ʴ�Ϊ����1��y=40.5-40cos$\frac{��}{6}$t��t��0
��2��20����
��3��2���Ӻ����ֵΪ40�ף�
���� ���⿼�������Ǻ�����ͼ������ʣ��漰ʵ��Ӧ�ã������е��⣮


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������P-ABC�У���֪AB��BC��PA��BC��PA=AB=BC=PB����D��E�ֱ�ΪPB��BC���е㣮
��ͼ������P-ABC�У���֪AB��BC��PA��BC��PA=AB=BC=PB����D��E�ֱ�ΪPB��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com