
分析 设对角线AC、BD相交于O点,根据平行四边形的性质与向量加法法则,得到$\overrightarrow{AC}$=2$\overrightarrow{AO}$=2($\overrightarrow{AE}+\overrightarrow{EO}$),代入$\overrightarrow{AE}$•$\overrightarrow{AC}$,展开后即可求得答案.
解答 解:如图,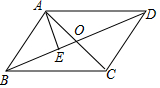
设对角线AC、BD相交于O点,
∵四边形ABCD是平行四边形,
∴$\overrightarrow{AC}=2\overrightarrow{AO}=2(\overrightarrow{AE}+\overrightarrow{EO})$,
因此,$\overrightarrow{AE}•\overrightarrow{AC}$=$\overrightarrow{AE}•2\overrightarrow{AO}$=2$\overrightarrow{AE}•(\overrightarrow{AE}+\overrightarrow{EO})$=2 ${\overrightarrow{AE}}^{2}+2\overrightarrow{AE}•\overrightarrow{EO}$,
∵|$\overrightarrow{AE}$|=2,$\overrightarrow{AE}⊥\overrightarrow{EO}$,
∴${\overrightarrow{AE}}^{2}=4$,$\overrightarrow{AE}•\overrightarrow{EO}=0$,
此可得$\overrightarrow{AE}•\overrightarrow{AC}=8$.
故答案为:8.
点评 本题在平行四边形中求向量的数量积,着重考查了平行四边形的性质、向量的线性运算性质、向量的数量积及其运算性质等知识,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤3} | B. | {x|3≤x<4} | C. | {x|0<x<4} | D. | {x|-4≤x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,2) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{6}{13}$ | B. | $\frac{6}{13}$ | C. | $-\frac{17}{13}$ | D. | $\frac{17}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{3}{2})<f(2)<f(3)$ | B. | $f(3)<f(2)<f(\frac{3}{2})$ | C. | $f(3)<f(\frac{3}{2})<f(2)$ | D. | $f(\frac{3}{2})<f(3)<f(2)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com