
分析 ①根据函数零点的存在条件进行判断即可.
②根据向量的数量积运算进行判断.
③根据函数奇偶性的定义以及充分条件和必要条件进行判断.
④根据含有量词的命题的否定进行判断即可.
解答 解:①函数f(x)=lnx-2+x在区间(1,e)上为增函数,
∵f(1)=ln1-2+1=-1<0,f(e)=lne-2+e=e-1>0,
∴函数f(x)在区间(1,e)上存在零点;
②在△ABC中,已知$\overrightarrow{AB}$•$\overrightarrow{AC}$=4,$\overrightarrow{AB}$•$\overrightarrow{BC}$=-12,
则$\overrightarrow{AB}$•$\overrightarrow{AC}$-$\overrightarrow{AB}$•$\overrightarrow{BC}$=16,
即$\overrightarrow{AB}$•($\overrightarrow{AC}$-$\overrightarrow{BC}$)=$\overrightarrow{AB}$•($\overrightarrow{CB}$-$\overrightarrow{CA}$)=$\overrightarrow{AB}$•$\overrightarrow{AB}$=16,
|$\overrightarrow{AB}$|=4;故②正确,
③若“函数$f(x)=\frac{{a-{e^x}}}{{1+a{e^x}}}$在定义域上是奇函数”,
则$f(-x)=\frac{a-{e}^{-x}}{1+a{e}^{-x}}$=$\frac{a{e}^{x}-1}{{e}^{x}+a}$=$-f(x)=-\frac{a-{e}^{x}}{1+a{e}^{x}}$,即解得a=±1,故“a=1”是函数$f(x)=\frac{{a-{e^x}}}{{1+a{e^x}}}$在定义域上是奇函数的充分不必要条件正确;故③正确,
④若命题p是:对任意的x∈R,都有sinx<1,则¬p为:存在x∈R,使得sinx≥1.故④错误,
故答案为:①②③.
点评 本题是命题的真假判断为载体考查了函数的零点,奇函数的定义,函数图象的平移,函数的对称性,是函数与逻辑的综合应用.综合性较强难度不大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
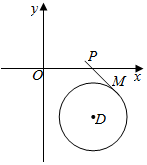 如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.
如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
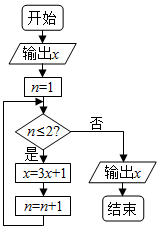 从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com