
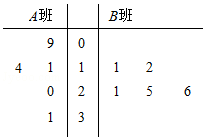
 某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).分析 (1)计算A、B班样本数据的平均值,比较即可得出结论;
(2)由A班的样本数据中不超过19的数据a有3个,
B班的样本数据中不超过21的数据b也有3个;
利用列举法求出从A班和B班的样本数据中各随机抽取一个的基本事件数,计算对应的概率.
解答 解:(1)A班样本数据的平均值为$\frac{1}{5}(9+11+14+20+31)=17$,
由此估计A班学生平均观看时间大约为17小时;
B班样本数据的平均值为$\frac{1}{5}(11+12+21+25+26)=19$,
由此估计B班学生平均观看时间较长;
(2)A班的样本数据中不超过19的数据a有3个,分别为:9,11,14;
B班的样本数据中不超过21的数据b有3个,分别为:11,12,21;
从A班和B班的样本数据中各随机抽取一个共有:9种不同情况,分别为:
(9,11),(9,12),(9,21),(11,11),(11,12),
(11,21),(14,11),(14,12),(14,21);
其中a>b的情况有(14,11),(14,12)两种,
故a>b的概率为P=$\frac{2}{9}$.
点评 本题考查了茎叶图以及平均数的应用问题,也考查了列举法求古典概型的概率问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | x=一$\frac{π}{6}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{24π}{25}$ | D. | x=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+y2=16 | B. | x2+(y-6)2=72 | C. | ${(x-\frac{8}{3})^2}+{y^2}=\frac{100}{9}$ | D. | ${(x+\frac{8}{3})^2}+{y^2}=\frac{100}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6,-8 | B. | -6,-9 | C. | -8,-9 | D. | 6,-9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
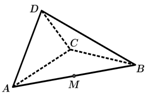 如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.
如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com