
分析 先判断直线直线l:x+y=1和圆C相离,设出P、Q的坐标,求得 $\overrightarrow{OP}$+$\overrightarrow{OQ}$ 的坐标,可得 $|\overrightarrow{OP}+\overrightarrow{OQ}|$的解析式,利用 $|\overrightarrow{OP}+\overrightarrow{OQ}|$ 的几何意义以及二次函数的性质求得它的最小值.
解答 解:圆心C(2,2)到直线l:x+y=1的距离为d=$\frac{|2+2-1|}{\sqrt{2}}$=$\frac{3}{\sqrt{2}}$>1,故直线直线l:x+y=1和圆C相离.
∵P为圆C:(x-2)2+(y-2)2=1上任一点,设P的坐标为(x,y),
∵Q为直线l:x+y=1上任一点,∴可设Q的坐标为(a,1-a),
∴$\overrightarrow{OP}$+$\overrightarrow{OQ}$=(x+a,y+1-a),∴$|\overrightarrow{OP}+\overrightarrow{OQ}|$=$\sqrt{{(x+a)}^{2}{+(y+1-a)}^{2}}$,
表示点(-a,a-1)到圆C:(x-2)2+(y-2)2=1上的点的距离.
设点(-a,a-1)到圆心C(2,2)的距离为d,则$|\overrightarrow{OP}+\overrightarrow{OQ}|$的最小值为d-1.
∵d=$\sqrt{{(-a-2)}^{2}{+(a-1-2)}^{2}}$=$\sqrt{{2a}^{2}-2a+13}$=$\sqrt{{2(a-\frac{1}{2})}^{2}+\frac{25}{2}}$,
故当a=$\frac{1}{2}$时,d最小为$\sqrt{\frac{25}{2}}$,故$|\overrightarrow{OP}+\overrightarrow{OQ}|$的最小值为d-1=$\frac{5\sqrt{2}}{2}$-1=$\frac{5\sqrt{2}-2}{2}$,
故答案为:$\frac{{5\sqrt{2}-2}}{2}$.
点评 本题主要考查直线和圆的位置关系,求向量的模,两点间的距离公式,二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}+\frac{3}{5}i$ | B. | $\frac{1}{5}-\frac{3}{5}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $-\frac{1}{5}-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
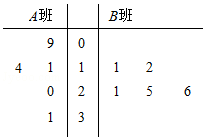 某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
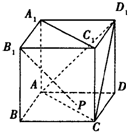 如图,正方体ABCD-A1B1C1D1的棱长为1,点P在四边形ABCD内及其边界上运动,且点P到点B1的距离为$\sqrt{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,点P在四边形ABCD内及其边界上运动,且点P到点B1的距离为$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com